Lab 1 (707)

Due: February 25, 2022 by 14:00 ET

LAB MATERIALS

Lab 1 Goals

• Estimate crude measures of (linear) association using univariable linear regression models
  
• Estimate crude measures of non-linear association using univariable linear regression models with linear transformed and categorical variables.
  
• Estimate adjusted measures of association using multivariable linear regression models

Data and assignment

The assignment and dataset are both available on Sakai.

Lab 1 Grading scheme

Competency	Points
Table 1a - Pearson CC	3
Table 1b - Spearman rank CC	3
Table 2 - Univariate models	10
Table 3 - F Statistic	3
Task 4 - Multivariable models	10
Figures	15 (1 point each)
Short answers 1 - 7	56 (8 points each)
Total	100

Packages

• {moments}
• {car}
• {tidyverse}

Competencies:

Import data from .csv

Comma separated values (.csv)

CSV stands for “comma separated values”. It’s a way of organizing data. When a file extension reads .csv, spreadsheet applications like Excel understand that to mean that the data are stored according to a simple set of rules.

See if you can spot the pattern.

The raw data might look like this:

Name, Date, App, date location, date ranking, second date
John, 01-19-2019, Bumble, sip and paint, 7, 0
Niko, 02-14-2019, Hinge, sky diving, 10, 0
Arwin, 02-28-2019, Bumble, ice skating, 8, 0
Chad, 03-12-2019, Tinder, movie night, 4, 0
Oleksiy, 03-15-2019, Bumble, axe throwing, 8, 0
Manuel, 03-19-2019, Bumble, bike ride, 9, 0
Vince, 03-27-2019, Ship, barcade, 7, 0
Adamu, 04-01-2019, Hinge, botanical garden, 8.5, 0 
Ryan, 04-21-2019, Christian mingle, mass, 7.5, 0

And a spreadsheet application (e.g. Microsoft Excel) would display the data like this: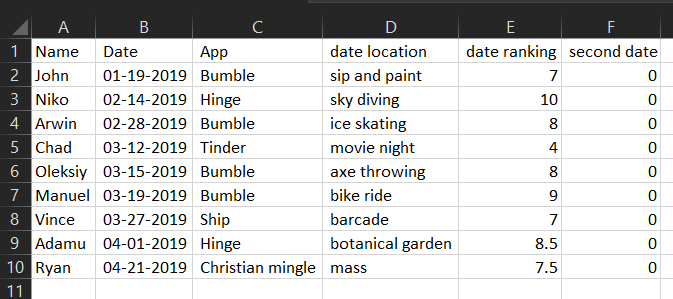

Which in R Studio, would look like this:

Name	Date	App	date location	date ranking	second date
John	01-19-2019	Bumble	sip and paint	6.9	0
Niko	02-14-2019	Hinge	sky diving	9.9	0
Arwin	02-28-2019	Bumble	ice skating	8.2	0
Chad	03-12-2019	Tinder	movie night	4.4	0
Oleksiy	03-15-2019	Bumble	axe throwing	8.3	0
Manuel	03-19-2019	Bumble	bike ride	8.9	0
Vince	03-27-2019	Ship	barcade	7.3	0
Adamu	04-01-2019	Hinge	botanical garden	8.5	0
Ryan	04-21-2019	Christian mingle	mass	7.5	0

Expand for the four simple rules of .csv data

• commas delineate columns

• a new line delineates a new row

• the first row of data determines column names and number of columns

• the values between commas are data

Import from .csv (read.csv())

read.csv() works a lot like readRDS(), except it can interact with .csv files.

Before you try to import your data, do yourself a favor and open the .csv file in Excel to inspect it.

The first 10 rows of regdat.csv

Now that you’ve done that, note that read.csv() allows the following arguments relevant to importing this lab’s data:

• file = "" - just like readRDS, you need to provide a file name in quotes
• header = - this argument takes either TRUE or FALSE. If set to TRUE, the function will use the first row of the data as the column names (“headers”)
• col.names = c() - takes a vector that is the same length as the number of columns in the dataset. It will use the values in this vector as the column names.

Here is an example:

data <- read.csv("regdat.csv", header = FALSE, 
                 col.names = c("columnA", "columnB", "columnC", "columnD"))

Don’t forget to use <- to assign a name to your imported data frame!

Plots with {ggplot2}

Histograms (geom_histogram())

If you need a refresher on creating histograms with {ggplot2}, you can find it here.

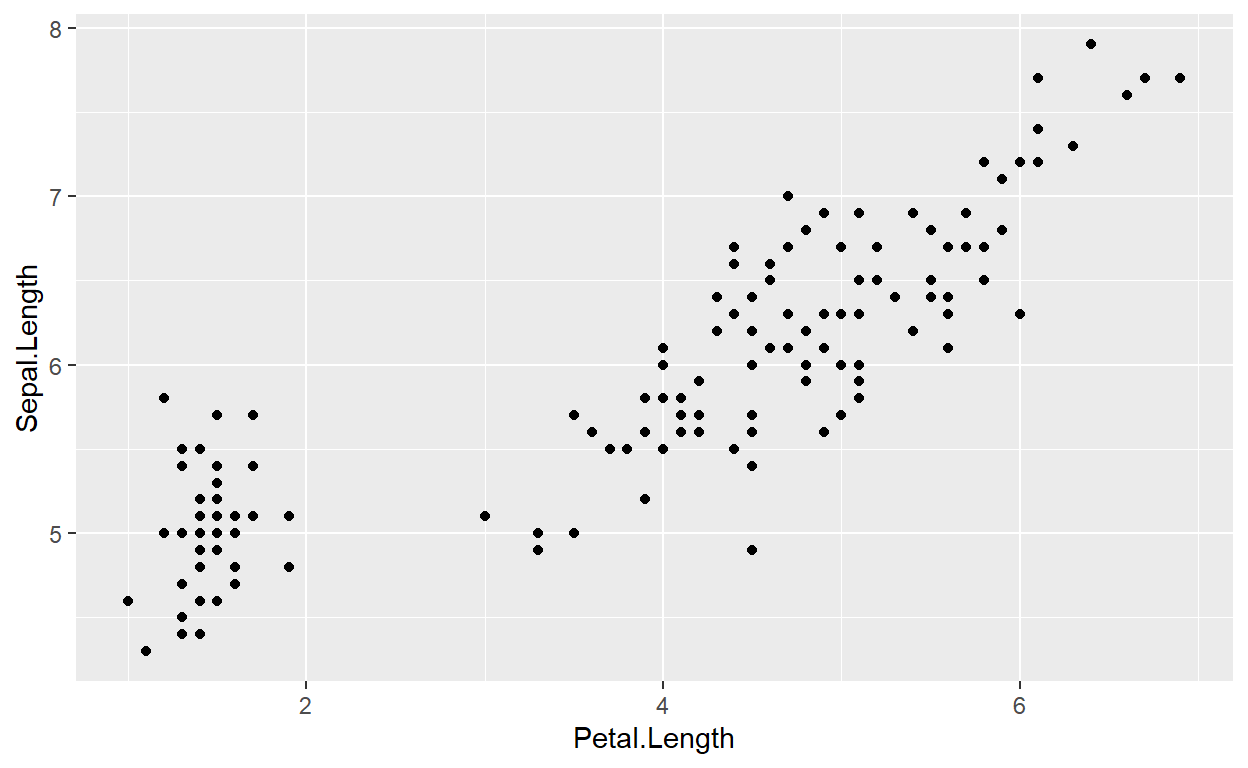
Scatter plots (geom_point())

We create scatter plots by assigning an x and y aesthetic (aes()) to a ggplot object, and then adding a layer called geom_point()

Q-Q Plots (qqnorm())

A Q-Q plot allows us to compare a variable’s observed distribution against its “theoretical” distribution. It does this by taking a continuous variable, converting each value to a Z-score (using the variable’s mean and standard deviation), and then plotting the Z-score against the original observed value.

To do this in R, we might start by creating a qqnorm object using qqnorm():

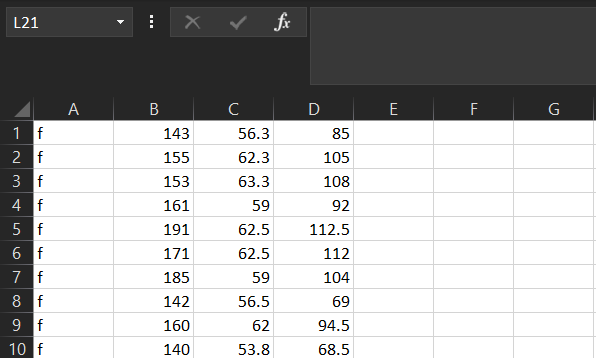
As an example, here are first 10 values of regdat$weight. “Observed Values” are the actual data, and “Z-values” are the Z-score for each of those values of weight:

Observed Values	Z Values
85.0	-0.6979123
105.0	0.1272606
108.0	0.2675710
92.0	-0.4018917
112.5	0.7389858
112.0	0.4482006
104.0	0.0847131
69.0	-1.9916133
94.5	-0.2348232
68.5	-2.0751279

We can use qqnorm() to calculate and plot these values automatically!

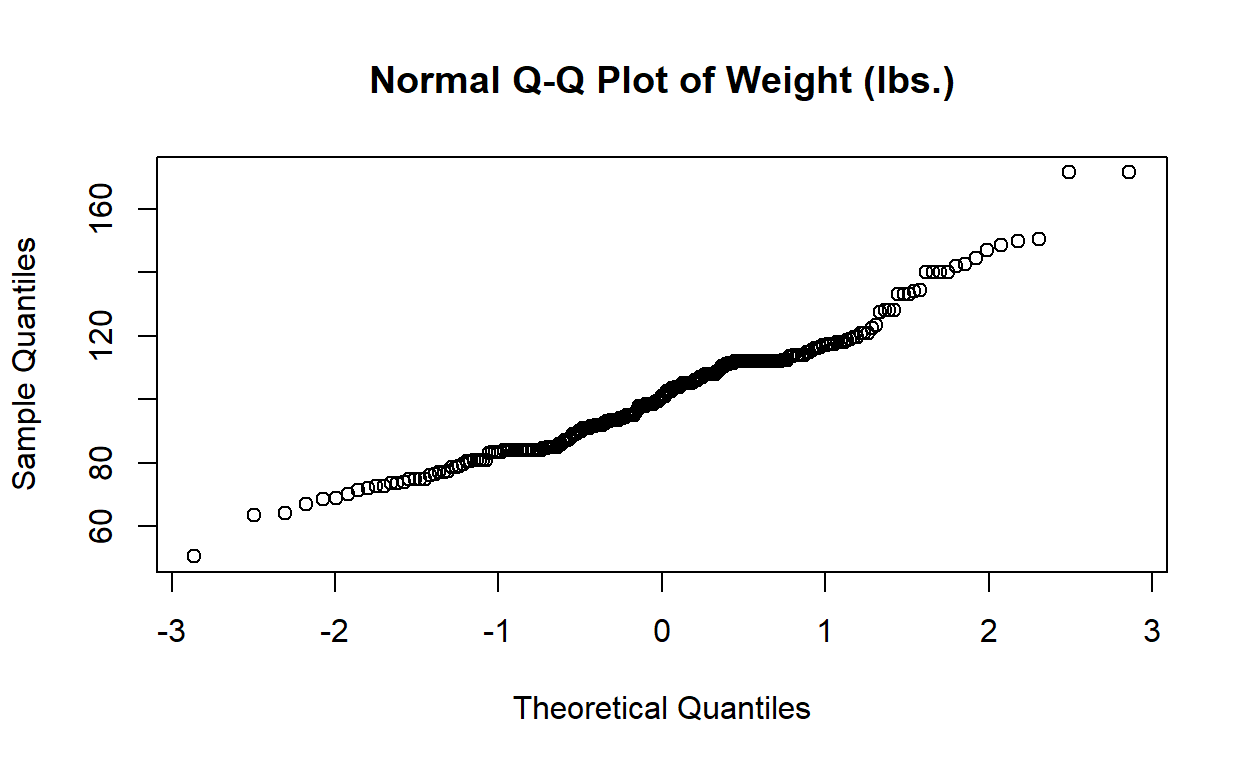
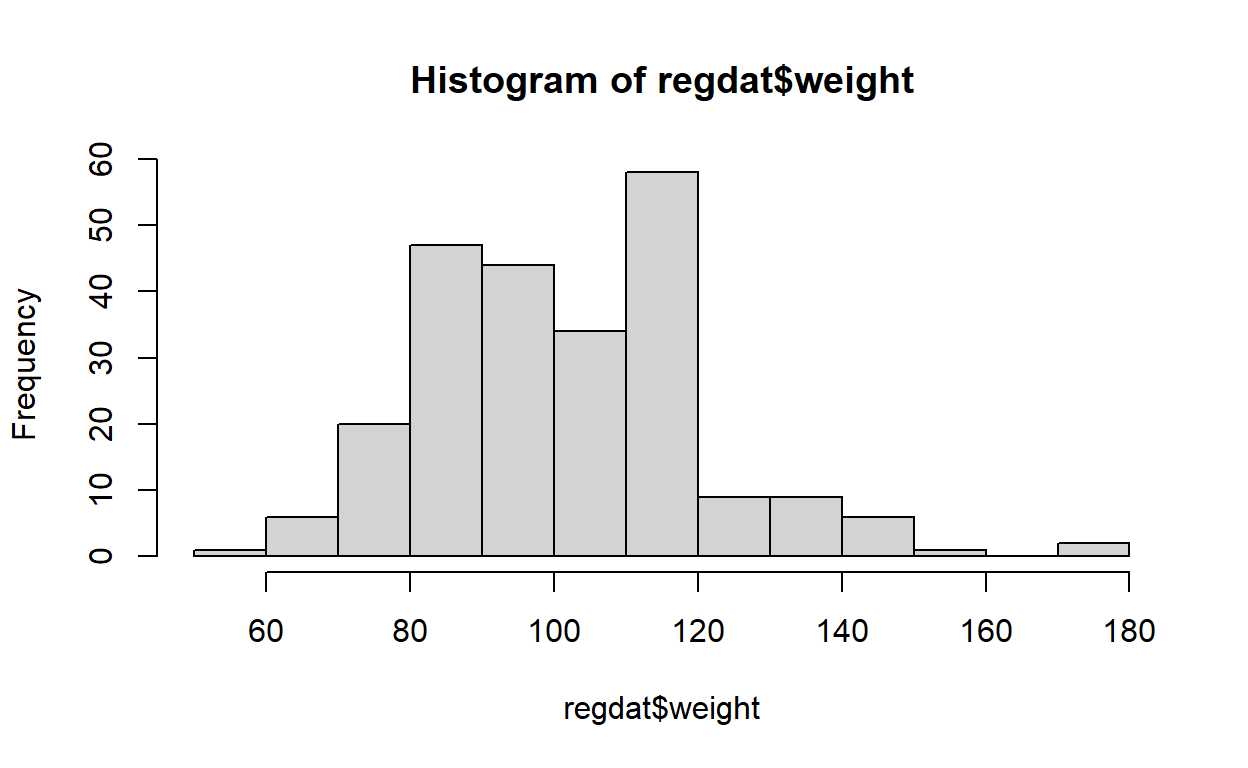
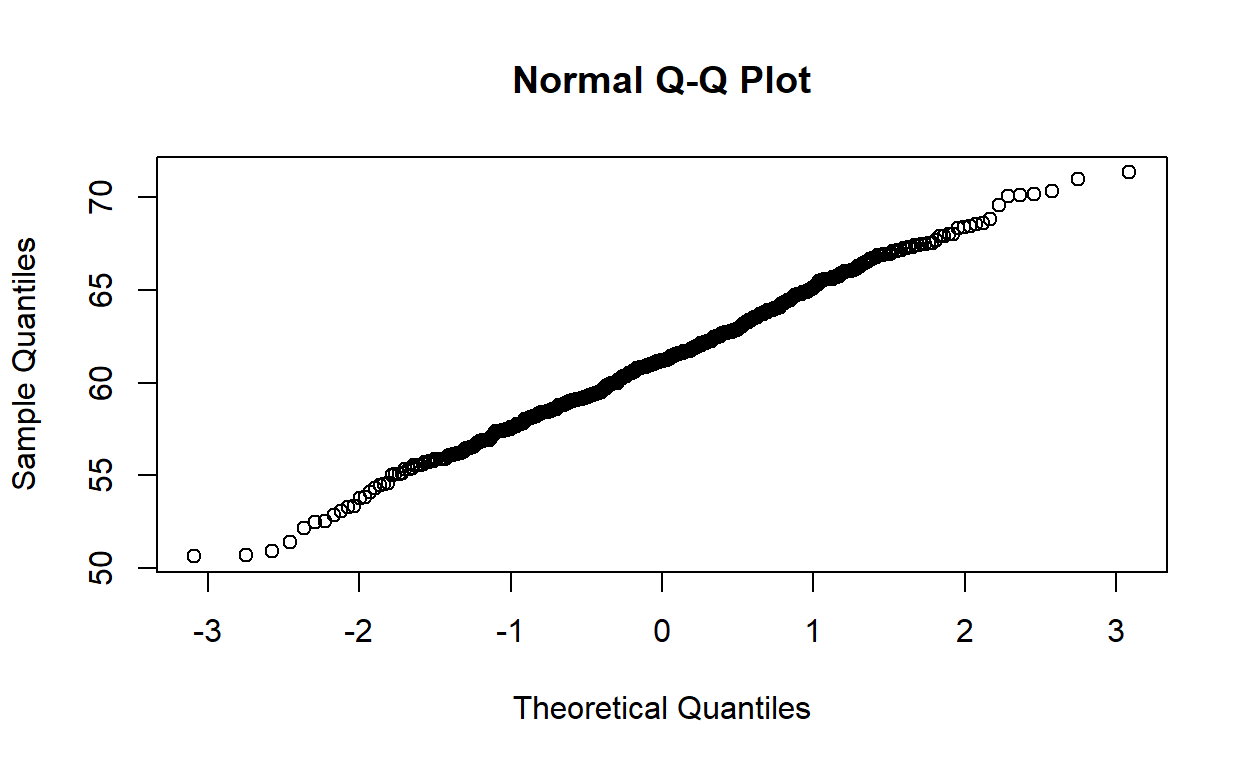
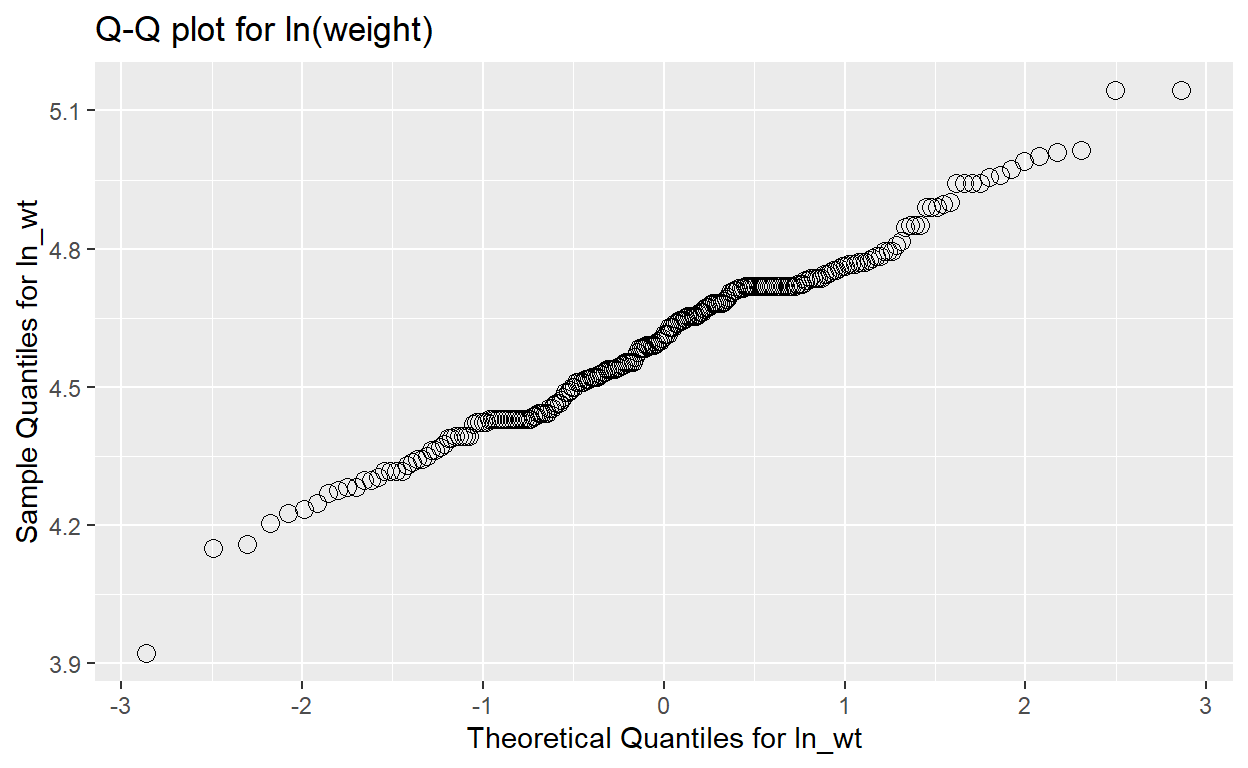
Here is the Q-Q plot for regdat$weight, with histogram for reference. Notice that the y-axis is labelled “Sample Quantiles” and its range is the minimum and maximum weight in regdat, while the x-axis is labelled “Theoretical Quantiles” and ranges from -3 to 3. Why might that be?

qqnorm(regdat$weight, main = "Normal Q-Q Plot of Weight (lbs.)")
hist(regdat$weight)

If weight were normally distributed, we would expect a straight diagonal line. See the “Note on Q-Q plots” below for an example of this.

Note on Q-Q Plots

For a quick comparison, we can use a simple model to visualize how a truly normal distribution would appear on a Q-Q plot:

This page from U Virginia is an excellent resource.

If we extract the mean and standard deviation from our height, we can construct a normal distribution and plot it.

# calculate mean of height
x_hat <- mean(regdat$height)
# calculate sd of height
x_sd <- sd(regdat$height)
# simulate a normal distribution using height's mean and sd
normal <- rnorm(500, mean = x_hat, sd = x_sd)
# scatter plot
plot(normal)
# histogram
hist(normal)
# Q-Q plot
qqnorm(normal)

Bonus: qqnorm(), but with ggplot()

For those interested:

Remember the discussion about how most objects contain more information than initially meets the eye?

The same goes for qqnorm objects. They aren’t just a bunch of dots. They contain vectors of the theoretical and observed (“Sampled”) quantiles. If we convert the qqnorm object to a data.frame, we can use ggplot() to call those specific columns for plotting. Let’s look at how we would make a Q-Q plot for the natural log of weight:

# calculate ln_wt
regdat$ln_wt <- log(regdat$weight)

# create qqnorm() object and convert to data.frame() object
qqnorm_data <- data.frame(qqnorm(regdat$ln_wt, plot.it = FALSE))

# plot in ggplot
ggplot(data = qqnorm_data, aes(x = x, y = y)) +
  geom_point(shape = 1, size = 3) + 
  labs(title = "Q-Q plot for ln(weight)") +
  xlab("Theoretical Quantiles for ln_wt") +
  ylab("Sample Quantiles for ln_wt")

Creating new variables

log() transform

In R, log() takes the natural log of a given value:

log(10)

[1] 2.302585

#> [1] 2.302585

If given a vector of values, log() will take the natural log of each of those values individually:

simple_vector <- c(1, 10, 100, 1000)

log(simple_vector)

#> [1] 0.000000 2.302585 4.605170 6.907755

Not relevant to Lab 01, but you can also specify what base you want your log to be in with the argument base =:

log(simple_vector, base = 10)

#> [1] 0 1 2 3

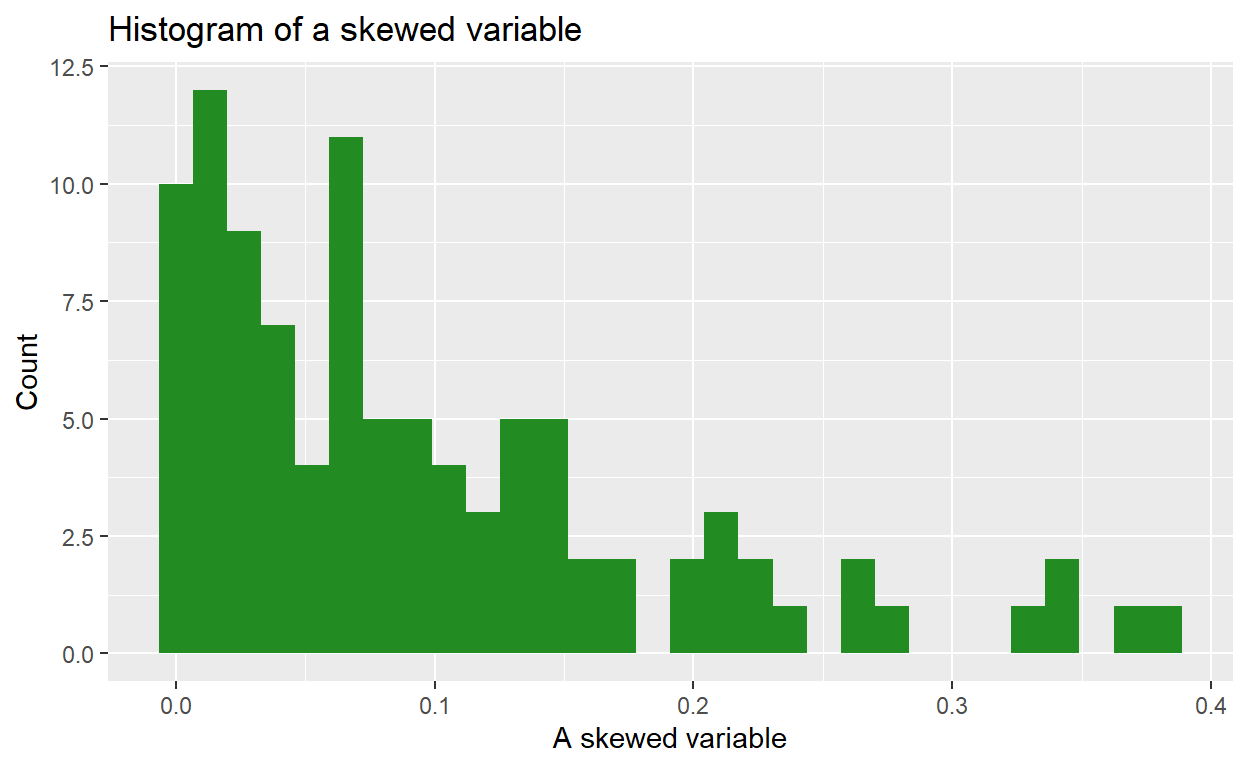
Why do a log transformation?

Imagine we have a variable that is highly right-skewed. The histogram of that variable might look something like this:

We can use a natural log transformation to make the variable’s distribution more “normal”, and therefore suitable for linear regression:

For more on transforming data into a normal distribution, see this link

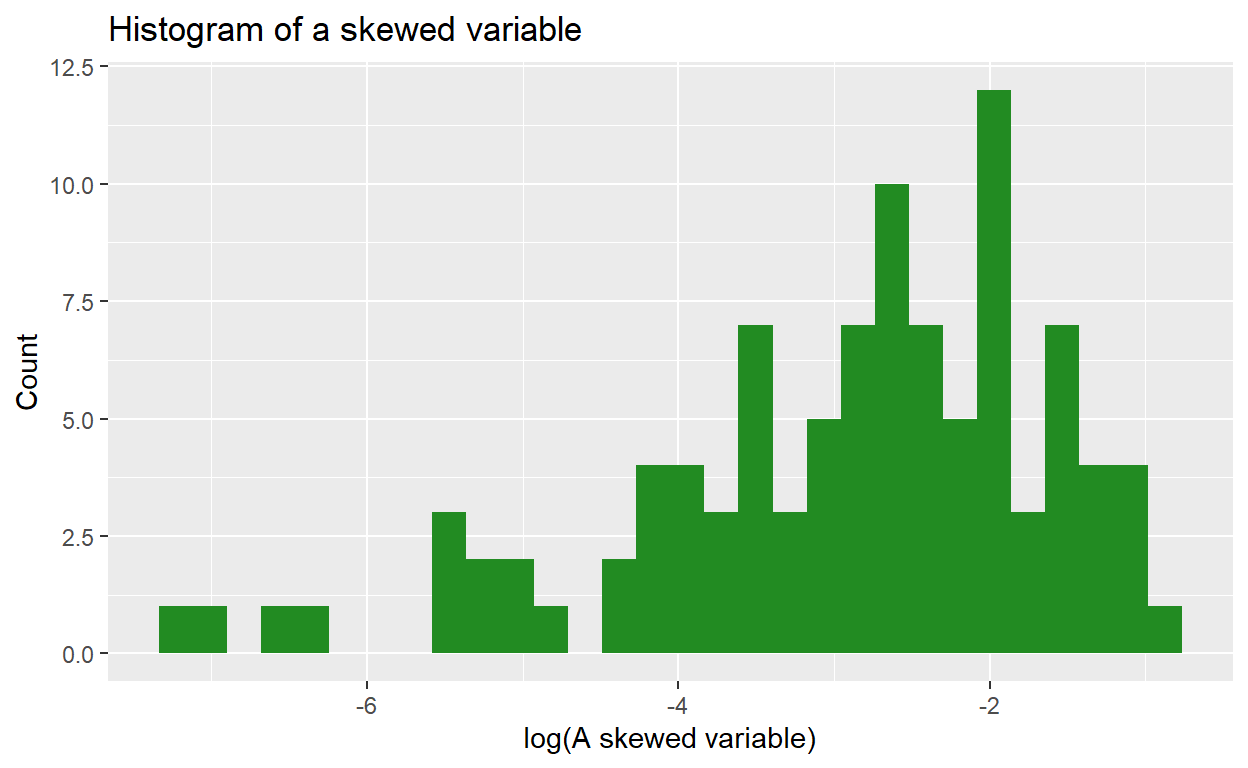
The natural log transformation uses ‘Euler’s number’ (2.718) as its ‘base’ (in contrast, a base 10 log transformation uses 10 as the base). So:

\[ \begin{eqnarray} ln(2) &=& 0.693\\ \rm{because} \ 2.718^.693 &=& 2 \end{eqnarray} \]

Using a log transformation can help to ‘pull in’ outlier values, which has the benefit of making the distribution more Normally distributed and reduce skew, although it doesn’t affect kurtosis.

Squaring with ^2

In R, you can raise a base by any exponent using ^. For example, 10³ would be written like this:

10^3

#> [1] 1000

If you give R a vector of numbers, followed by an exponent, it will perform the operation on each value individually:

simple_vector <- c(3, 3.3, 12, 1)
simple_vector^2

#> [1]   9.00  10.89 144.00   1.00

Recall that data frames are just lists of vectors!

You might consider using %>% and mutate() to create a squared variable.

Categorical variables with case_when()

For a refresher on how to generate categorical variables from continuous variables, you can refer back to when we created magec in last 705, Lab 0.

Skewness and Kurtosis ({moments} package)

In evaluating the skewness and kurtosis values, a variable that is perfectly normally distributed will have a skewness of 0 and a kurtosis of 3.

So for example, if a variable has a skewness of -0.05 and a kurtosis of 2.2, we would conclude that the data are slightly left skewed (negative value) and there is some kurtosis.

More specifically, because kurstosis, 2.2 < 3, we conclude that there are less data in the tails. If the value for kurtosis had been greater than 3, we would have concluded that the variable has more data in the tails than expected under a normal distribution.

Here is a link if you’d like to read more about it.

In R, we can calculate both skewness and kurtosis using a package called {moments} and its handy functions skewness() and kurtosis():

skewness(regdat$weight)

kurtosis(regdat$weight)

#> [1] 0.5843876
#> [1] 3.765937

You will need to install {moments} with install.packages("moments")

Pearson and Spearman rank correlation coefficients

We use correlation coefficients to measure the strength and direction of the linear association between two continuous variables.

Correlation coefficients can range from -1 to 1. Values closer to 1 represent a strong positive correlation. Those closer to -1 represent a strong negative correlation. The closer the correlation coefficient, R, is to 0, the weaker the association between the two variables.

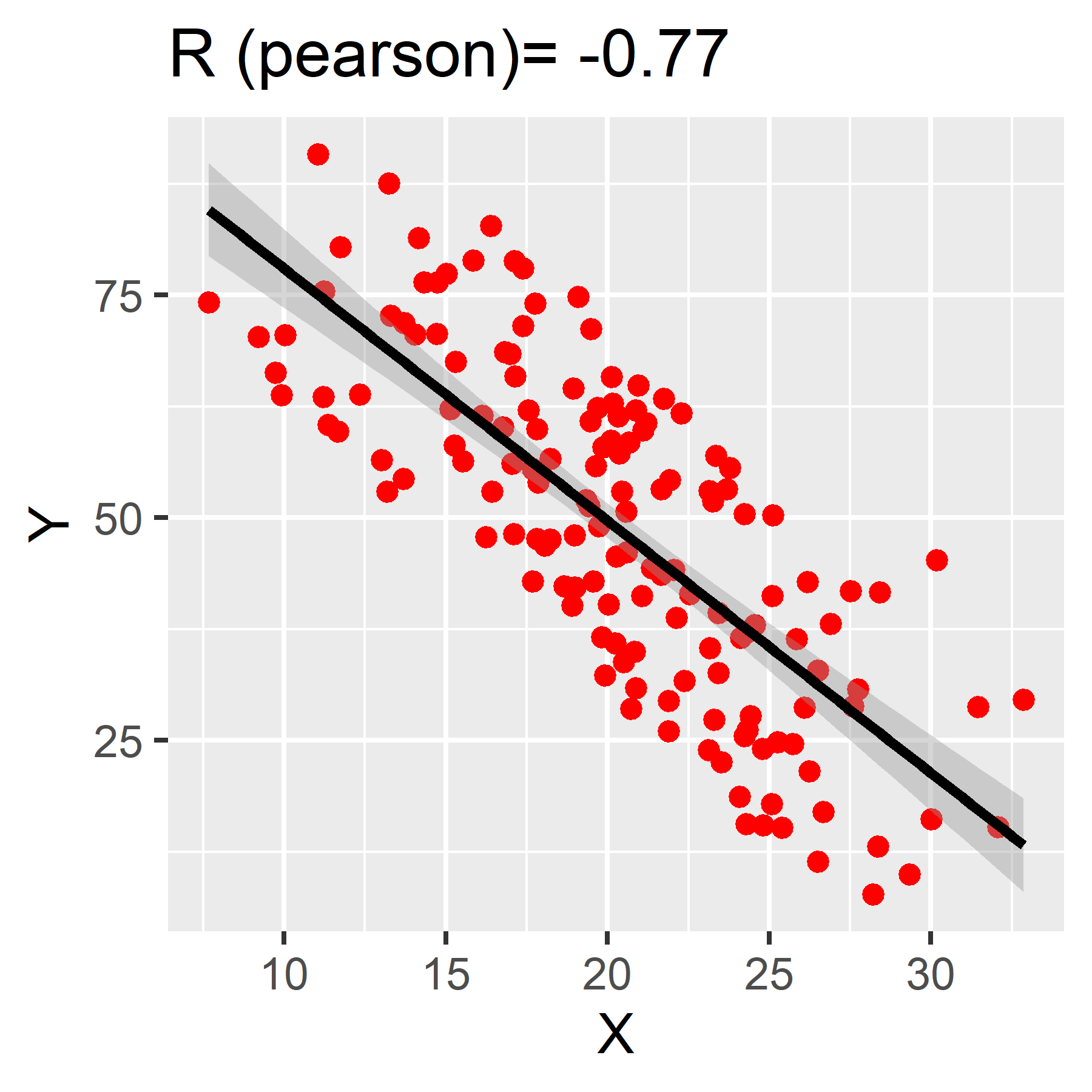
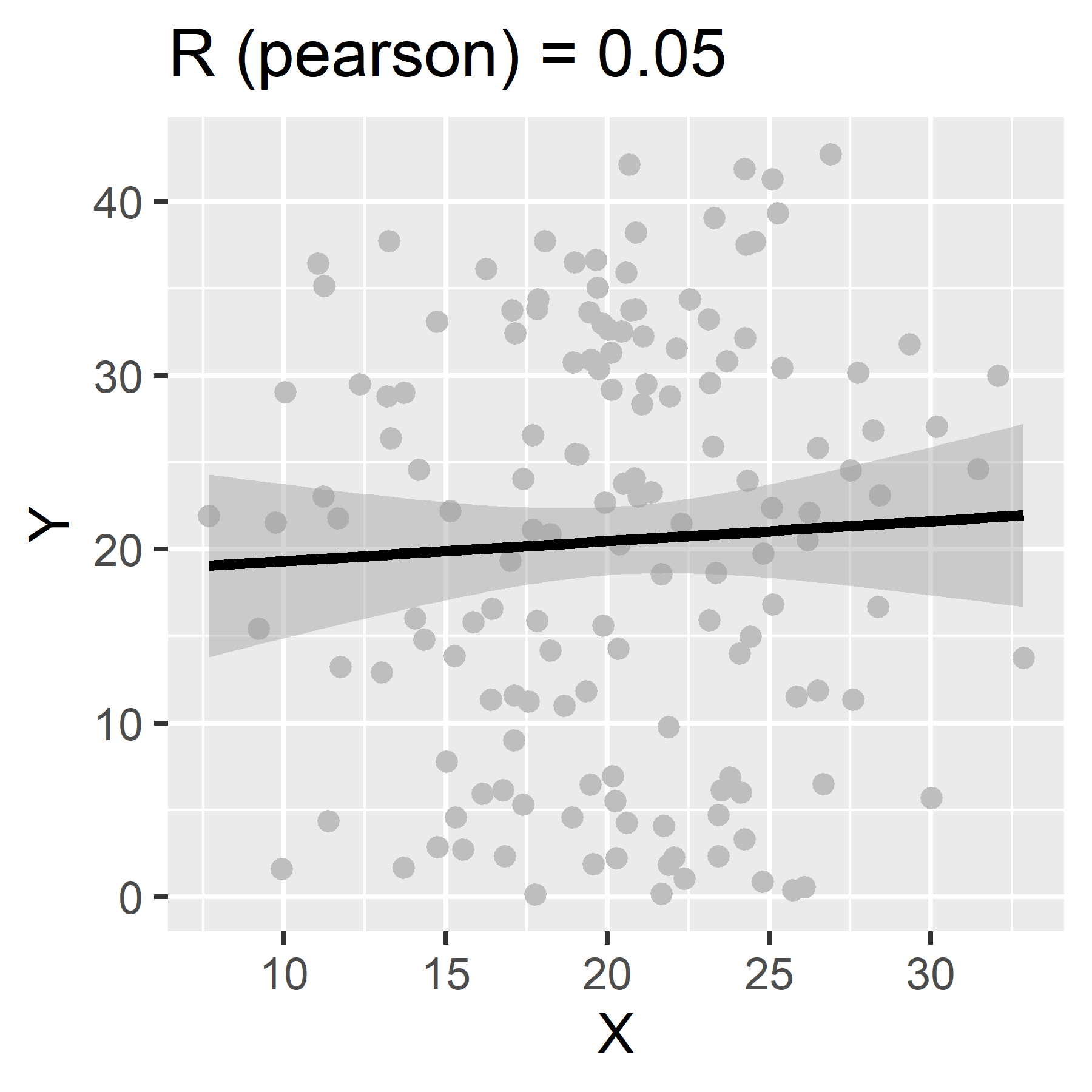
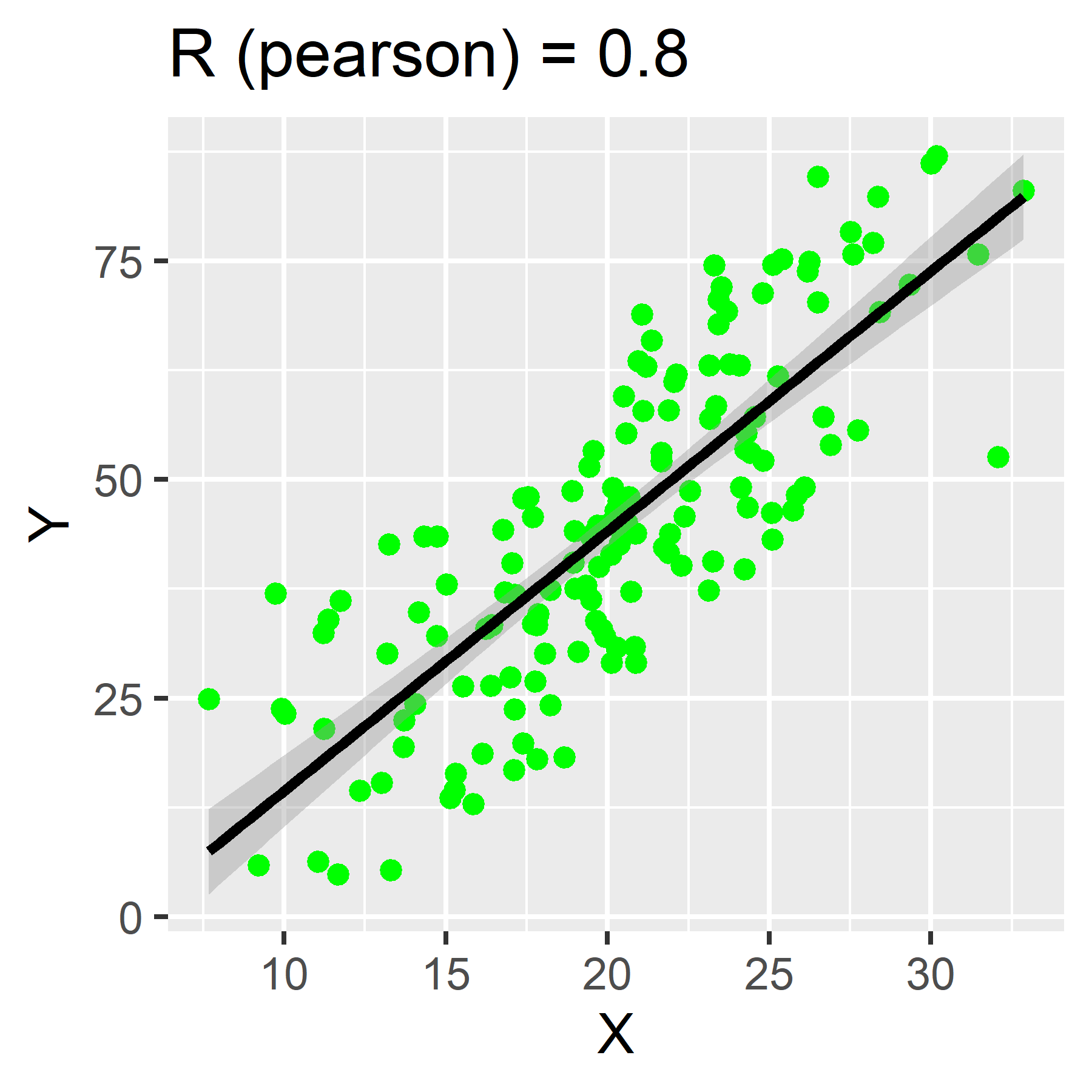
To calculate in R, use the function:

cor(x, y, 
    method = c("pearson", "kendall", "spearman"))` 

Specify your x and y variables and set the method to your cheeky brit of choice.

The Pearson is the parametric test. Both Spearman and Kendall refer to rank-based (non-parametric) measures of association for when our data are non-normal.

If no method is specified, “pearson” is the default.

Bonus: Correlation coefficient matrices

If you want to have a very particular kind of fun, try the following:

1. Take your regdat data and create a new data frame of only continuous variables from regdat. Give it a new name, like cont_data.
   
2. Use R to run cor(cont_data), where the data frame of continuous variable vectors is the only argument.

You can use {dplyr}’s select() to remove variables by name. But there are also many many ways to do this.

What did it do? (Go look at Table 1 in the assignment.)

Linear Regression Models

Building models in R is fun!

Univariate (single-variable) models with lm()

Remember the concept of R formulas?

Regression models make use of formulas in a very intuitive way. Here is the general format:

lm(response_var ~ predictor_var, data = a_data_frame)

lm stands for “linear model”. If we assign a name to our model, we can access various components within the model, which we can index with $.

We can also just use summary() to view an overview of the model’s most important components.

m1 <- lm(Sepal.Length ~ Petal.Length, data = iris)
summary(m1)

Call:
lm(formula = Sepal.Length ~ Petal.Length, data = iris)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.24675 -0.29657 -0.01515  0.27676  1.00269 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   4.30660    0.07839   54.94   <2e-16 ***
Petal.Length  0.40892    0.01889   21.65   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4071 on 148 degrees of freedom
Multiple R-squared:   0.76, Adjusted R-squared:  0.7583 
F-statistic: 468.6 on 1 and 148 DF,  p-value: < 2.2e-16

Multivariable models with lm()

You can also use lm() to program models with multiple linear predictor variables. You can formulate your equation as you build your model, using arithmetic operators on the right-hand side of the formula:

lm(response_var ~ predictor_var1 + predictor_var2, data = a_data_frame)

mlm1 <- lm(Sepal.Length ~ Petal.Length + Species, data = iris)

summary(mlm1)

Call:
lm(formula = Sepal.Length ~ Petal.Length + Species, data = iris)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.75310 -0.23142 -0.00081  0.23085  1.03100 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)        3.68353    0.10610  34.719  < 2e-16 ***
Petal.Length       0.90456    0.06479  13.962  < 2e-16 ***
Speciesversicolor -1.60097    0.19347  -8.275 7.37e-14 ***
Speciesvirginica  -2.11767    0.27346  -7.744 1.48e-12 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.338 on 146 degrees of freedom
Multiple R-squared:  0.8367,    Adjusted R-squared:  0.8334 
F-statistic: 249.4 on 3 and 146 DF,  p-value: < 2.2e-16

Linear models: a brief tour

In this section, we’ll show you how to access a model’s coefficients, confidence intervals, residuals, and other values that might come in handy.

Remember how we said that you can extract numbers from your model when you assign it a name? If we inspect m1 using $ to index the object by name, we’ll see some useful items at our disposal.

You can obtain the model’s coefficients with coef(your_model). For example:

coef(m1)

 (Intercept) Petal.Length 
   4.3066034    0.4089223 

And you can calculate 95% confidence intervals with confint(your_model, level = 0.95). For example:

confint(m1,  level = .95)

                 2.5 %    97.5 %
(Intercept)  4.1516972 4.4615096
Petal.Length 0.3715907 0.4462539

And don’t forget that you can inspect your model with summary():

summary(m1)

Call:
lm(formula = Sepal.Length ~ Petal.Length, data = iris)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.24675 -0.29657 -0.01515  0.27676  1.00269 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   4.30660    0.07839   54.94   <2e-16 ***
Petal.Length  0.40892    0.01889   21.65   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4071 on 148 degrees of freedom
Multiple R-squared:   0.76, Adjusted R-squared:  0.7583 
F-statistic: 468.6 on 1 and 148 DF,  p-value: < 2.2e-16

Our model contains the columns of data (variables) used in its calculation:

head(m1$model)

  Sepal.Length Petal.Length
1          5.1          1.4
2          4.9          1.4
3          4.7          1.3
4          4.6          1.5
5          5.0          1.4
6          5.4          1.7

It also has the resulting fitted values:

head(m1$fitted.values)

       1        2        3        4        5        6 
4.879095 4.879095 4.838202 4.919987 4.879095 5.001771 

The fitted values are what result when we plug each row into the model equation. We can use the first row of our data to observe this directly:

x <- m1$model[1,2] # Petal.Length of row 1

B0 <- m1$coefficients[1] # beta-naught

B1 <- m1$coefficients[2] # beta-one

# formula:
fitted <- B0 + B1 * x
fitted

(Intercept) 
   4.879095 

The resulting value is the “fitted” value, or the estimate of the response variable according to our model, given the value of the predictor, Petal.Length (which for the first row in our data, is 1.4).

Notice that our model also contains residuals, or the differences between our observed values for y (our response variable), and the values predicted by our model:

head(m1$residuals)

         1          2          3          4          5          6 
 0.2209054  0.0209054 -0.1382024 -0.3199868  0.1209054  0.3982287 

We can find the first row’s residual value with the fitted value that we calculated above:

# observed Sepal.Length of row 1 minus the predicted/fitted value:
m1$model[1,1] - fitted

(Intercept) 
  0.2209054 

Plotting line of best fit

{ggplot2} provides a wide variety of flexible tools for visualizing models. There are two main ways we might visualize a regression model. The best way to do this is to fit the model and then plot the prediction (often referred to as the line of best fit)

You can also use functions within {ggplot2} to generate a line of best fit. This is a technique that we will encounter later in the semester that is handy in special circumstances. But for now, please use the method that follows.

Here is a highly useful tutorial for how to plot different models in {ggplot2}. It includes splines, Loess, and multiple variations on quadratics.

Model first, then plot

We can plot our data and line of best fit by using a model as the data object required by {ggplot2}.

Remember our example model from earlier:

Call:
lm(formula = Sepal.Length ~ Petal.Length, data = iris)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.24675 -0.29657 -0.01515  0.27676  1.00269 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   4.30660    0.07839   54.94   <2e-16 ***
Petal.Length  0.40892    0.01889   21.65   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4071 on 148 degrees of freedom
Multiple R-squared:   0.76, Adjusted R-squared:  0.7583 
F-statistic: 468.6 on 1 and 148 DF,  p-value: < 2.2e-16

m1 will serve as our data object within ggplot(). We can start by creating a scatter plot of the response and predictor variables from our formula. But instead of using the original data frame (regdat), we’ll use data = m1:

p <- ggplot(data = m1, aes(x = Petal.Length, y = Sepal.Length)) +
  geom_point()

p

Notice that we have assigned a name to our plot, p. By doing this, we can add layers to the original plot without needing to reproduce the code each time.

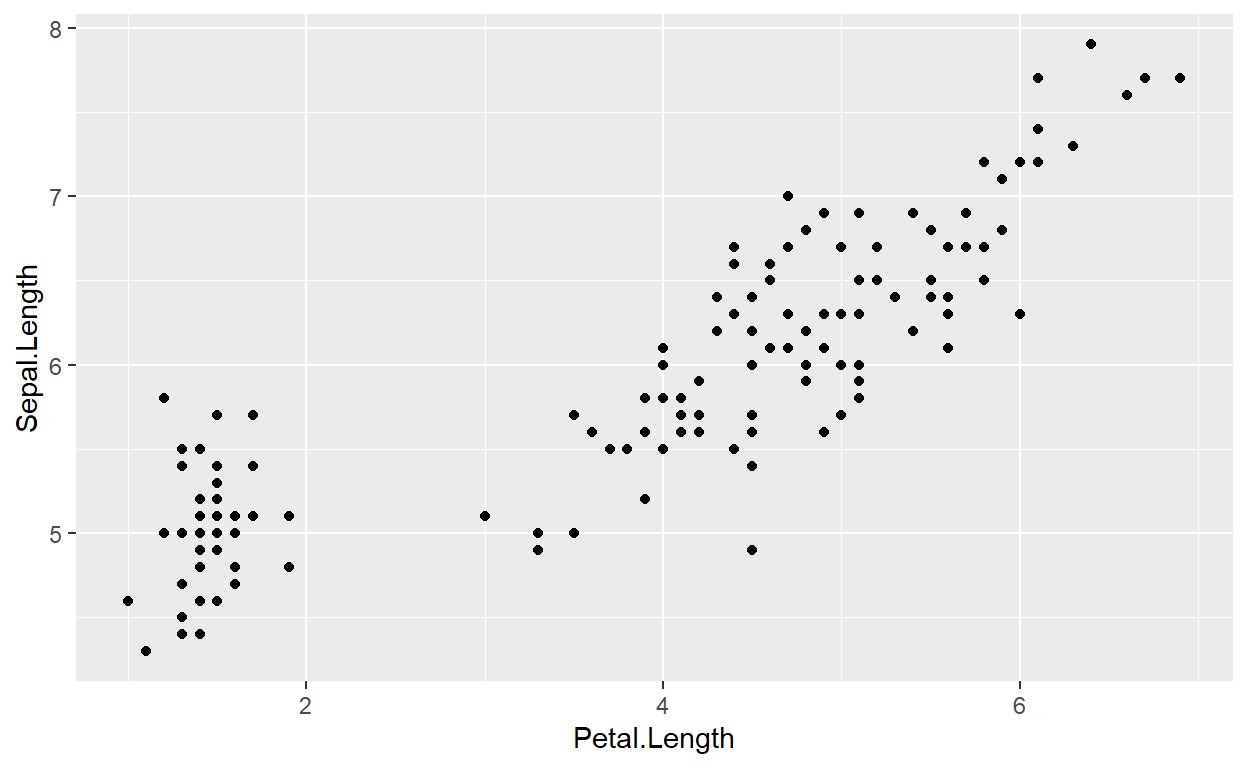
From here, we can add a geom_smooth() layer to fit an ordinary least squares regression line to our data. Notice that within the model m1, we have access to a variable, .fitted. We need to assign this to the y-axis of our plot. This will plot a line for Petal.Length against our fitted/predicted values!

p + geom_smooth(aes(y = .fitted))

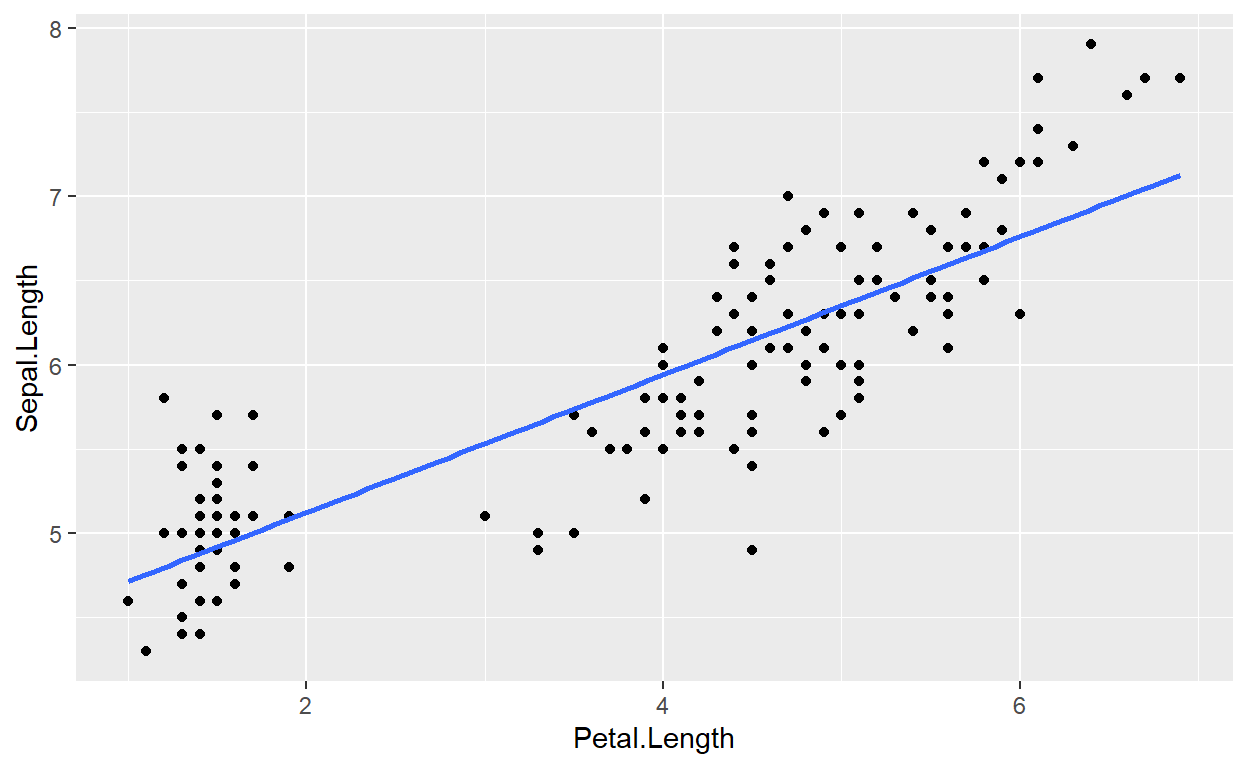
Understanding how this method works will become more important as our models increase in complexity. It also will helps in plotting residuals (see next section).

Plot first, then model

To perform this method, we need to start with a scatter plot using {ggplot2}:

p2 <- ggplot(data = toy, aes(x = ran1, y = pos)) +
  geom_point() +
  labs(x = "Age (years)", y = "Points", title = "This is fake data")

p2

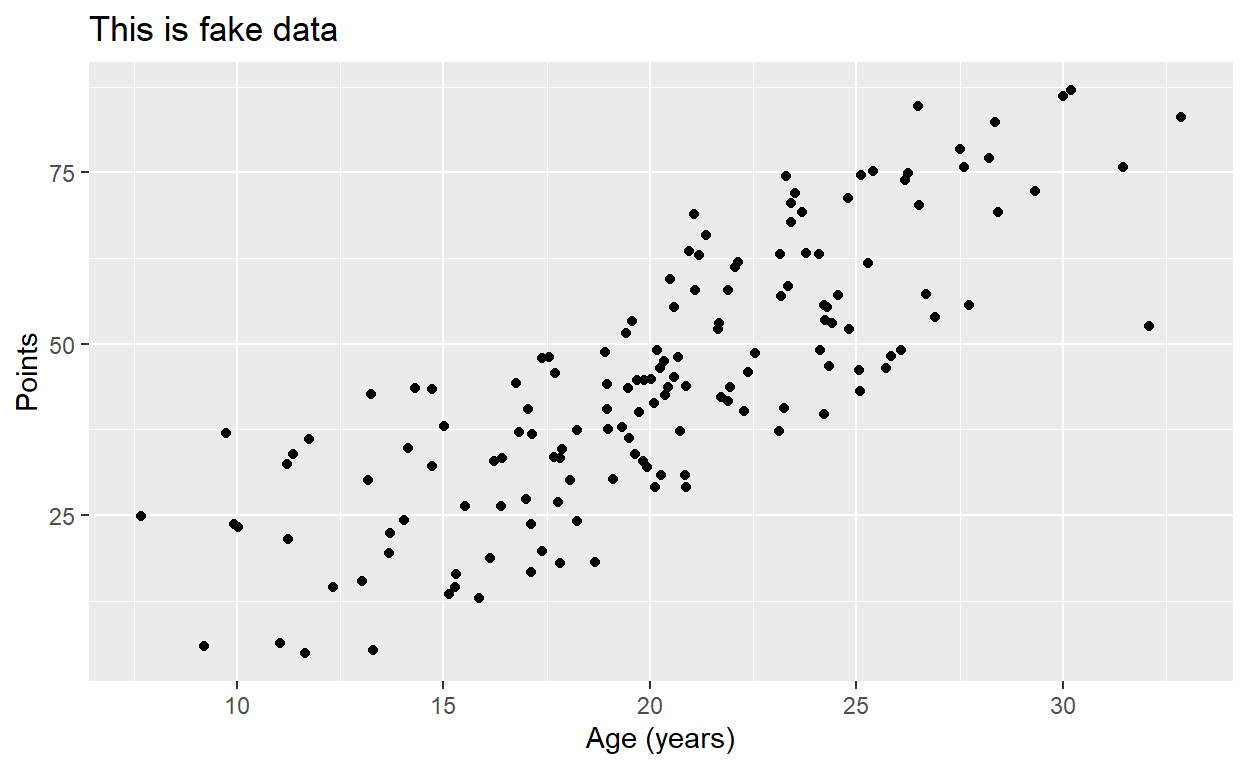
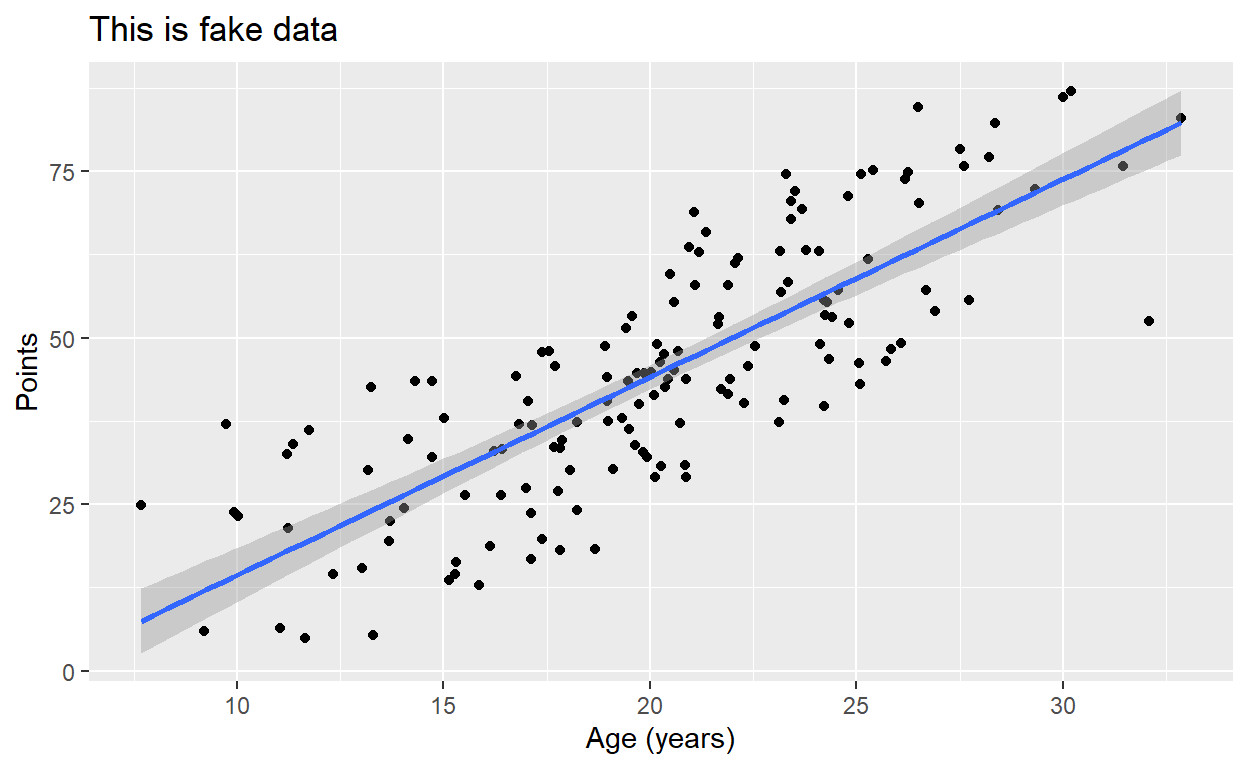
Once we have our plot, we just need to add another layer, stat_smooth(), and designate a method and formula. Here, we’re building a univariate, linear model. Observe how we parameterize these details within the stat_smooth() function:

p2 + stat_smooth(method = "lm", formula = y ~ x)

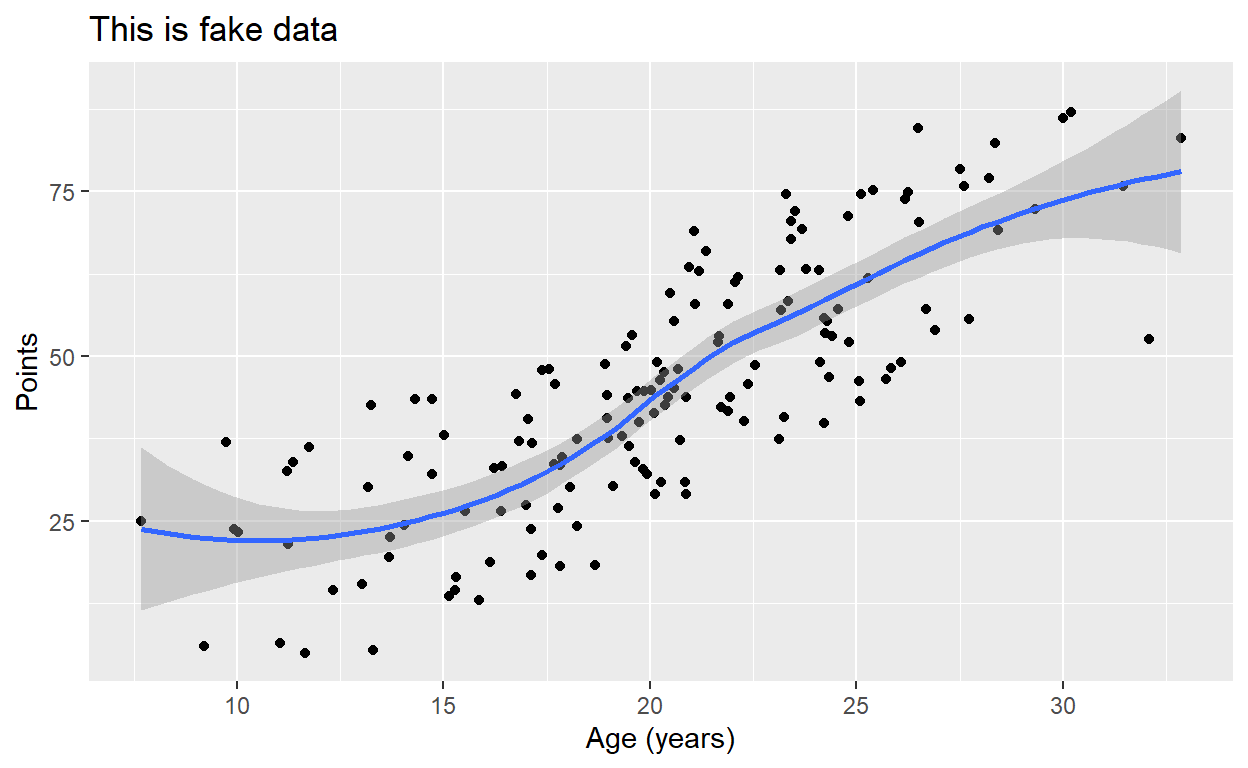
Notice that if we don’t designate a method, stat_smooth() will default to plotting a smoothed “loess” line, which we’ll learn more about later in the semester:

p2 + stat_smooth(formula = y ~ x)

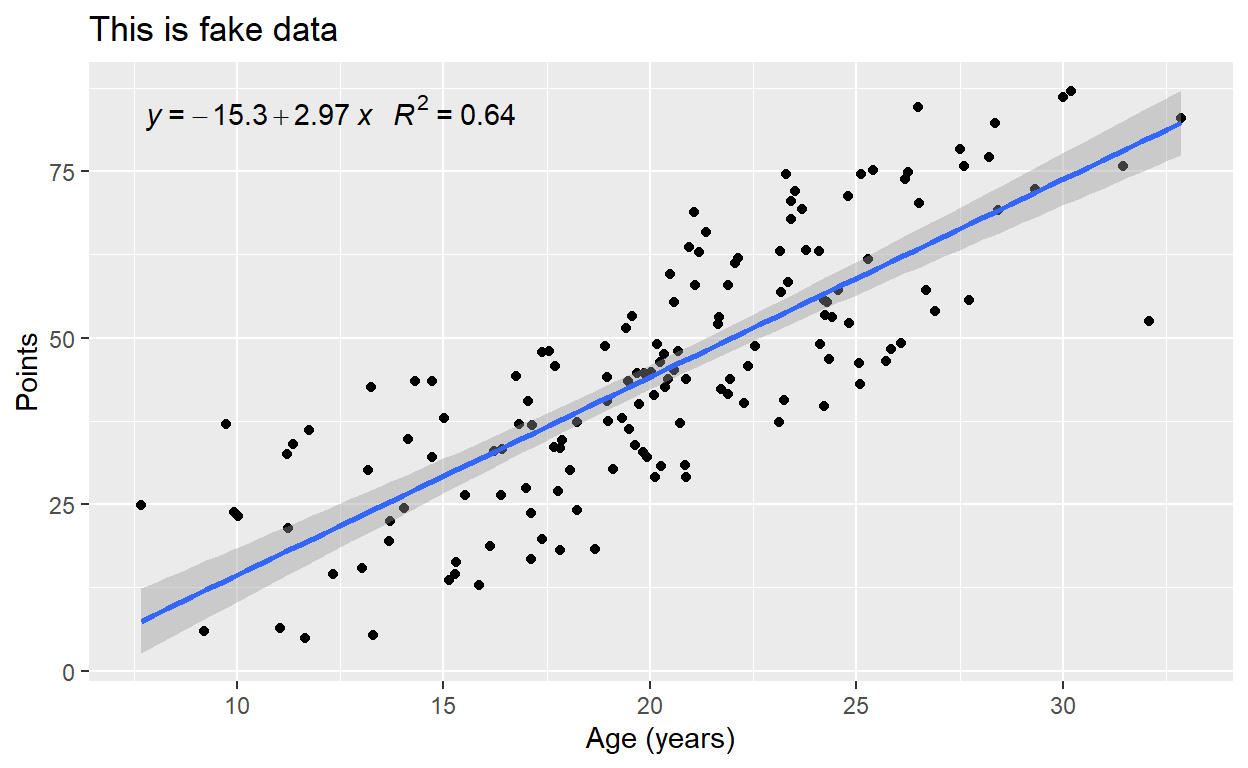
For those curious, we can also print our model’s equation in the plot. The code is a bit dense, but straightforward:

require(ggpmisc)

p2 + stat_smooth(method = "lm", formula = y ~ x) +
  stat_poly_eq(formula = y ~ x, 
                aes(label = paste(..eq.label.., 
                                  ..rr.label.., 
                                  sep = "~~~")), 
                parse = TRUE)

From this post on SO.

Model Evaluation

Once we’ve built a model, there are various measures we might use to evaluate how well that model fits our data. Here we discuss two of those measures: residuals and heteroscedasticity.

Residuals plots

Our model object contains a vector of residuals, which are the observed Y minus the predicted Y:

head(m1$residuals)

         1          2          3          4          5          6 
 0.2209054  0.0209054 -0.1382024 -0.3199868  0.1209054  0.3982287 

We could generate a histogram of our residuals. In the following code, notice that {ggplot2} finds our residuals when we refer to them as .resid:

ggplot(data = m1, aes(x = .resid)) + 
  geom_histogram(binwidth = .1, fill = "seagreen") +
  xlab('Residuals') +
  ggtitle("Histogram of residuals of Iris Petal Length regressed on Sepal Length")

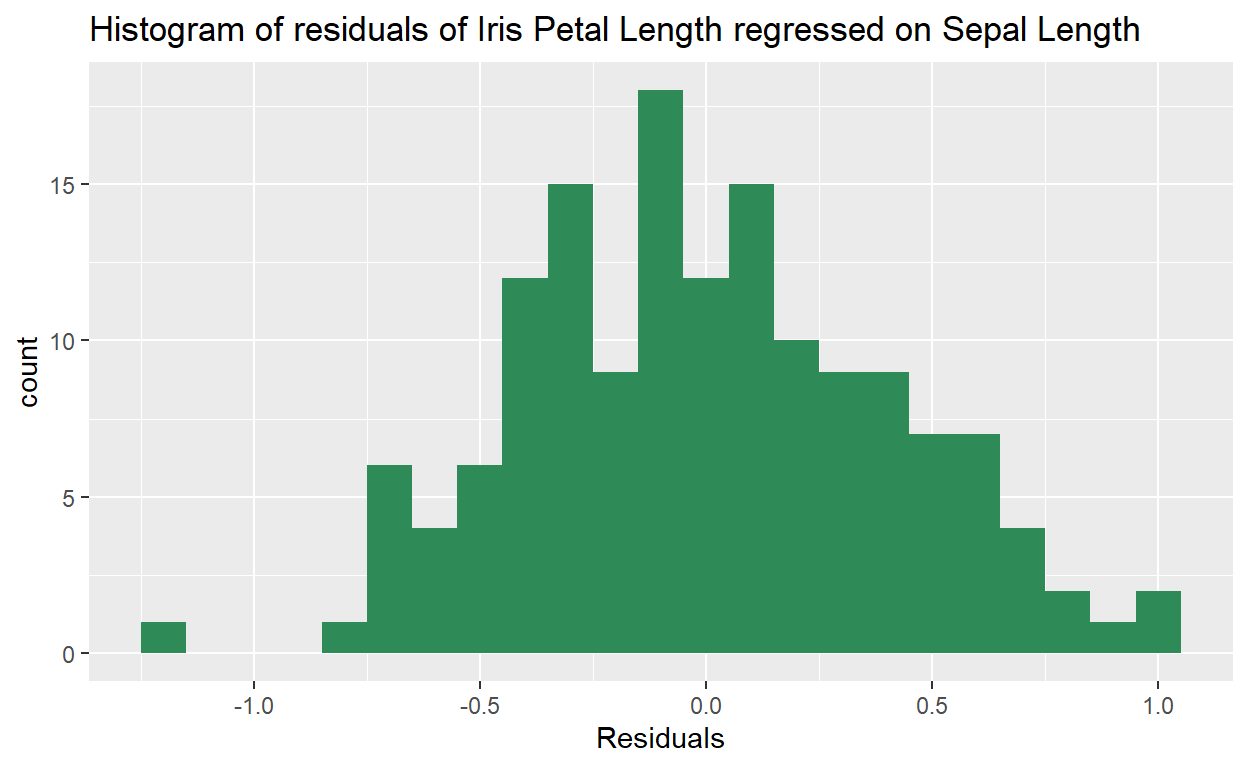
But we can also use that vector of residuals, .resid to create a scatter plot of our fitted data against our residuals:

ggplot(data = m1, aes(x = .fitted, y = .resid)) +
  geom_point() +
  geom_hline(yintercept = 0, linetype = "dashed") +
  labs(x = "Fitted values", 
       y = "Residuals", 
       title = "Residual plot of iris petal length regressed on sepal length")

Notice that we have added a dashed horizontal line at y = 0 by adding a layer to our plot: + geom_hline(yintercept = 0, linetype = "dashed")

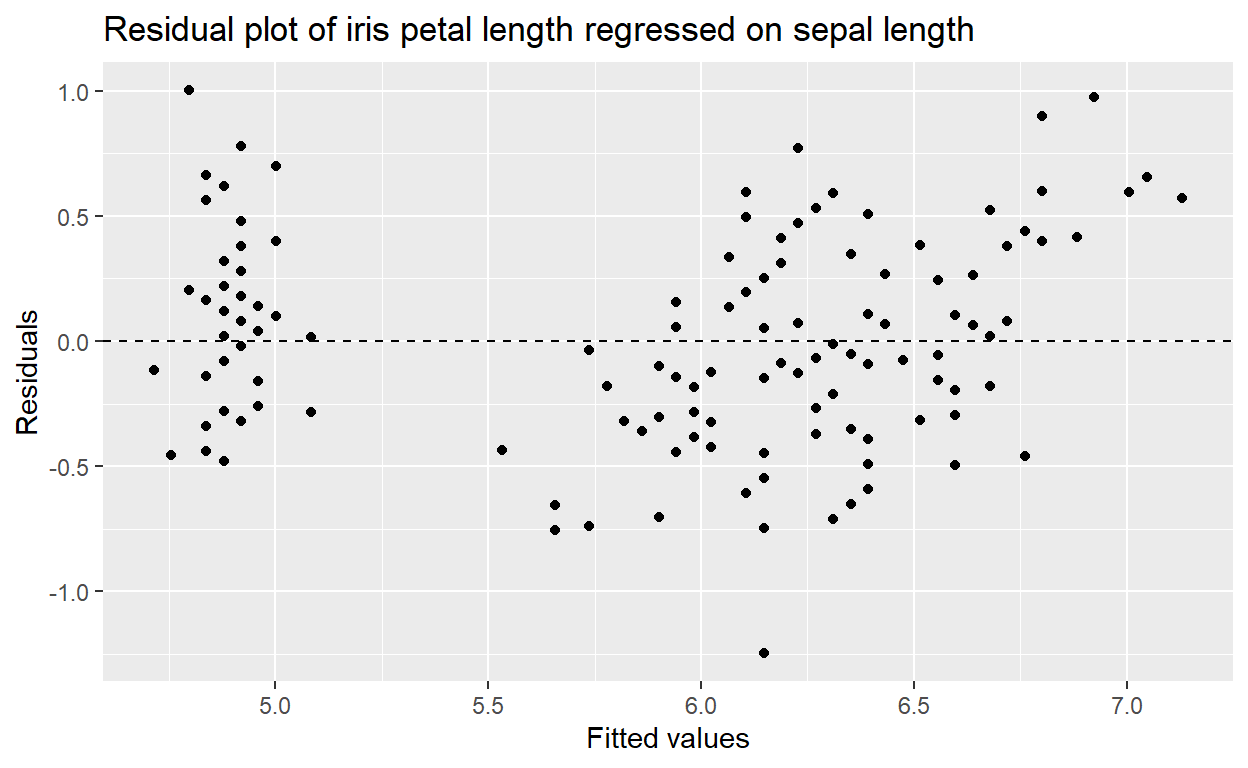
This tells us if there is any bias in our model’s fit.

One such trend we might observe is heteroskedasticity,

Heteroskedasticity

Simply put, heteroskedasticity is when the variability of Y (our response variable) is different depending on X (our predictor variable).

In the following plot, where along the x-axis would we be able to accurately predict Y using a linear model?

ggplot(het, aes(x = x, y = z)) +
  geom_point() +
  labs(x = "X", y = "Y", title = "More fake data")

Wikipedia is telling me that this is Greek for “different” (hetero) “dispersion” (skedasis)

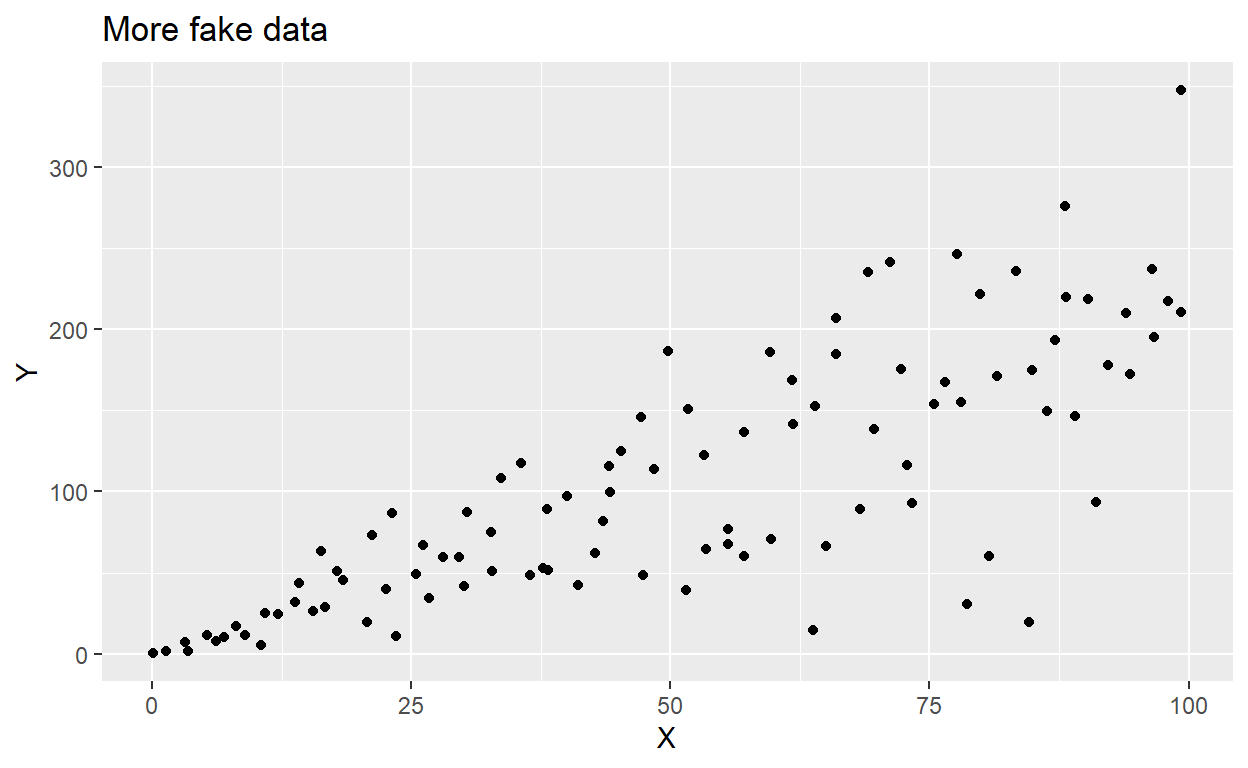
The data above are heteroskedastilisticexpialidocious.

Link, for the Disney lovers

Breusch-Pagan/Cook-Weisberg

We can use a chi-squared test to assess how heteroskedastic our data really are. We can do this using ncvTest() from the package {car}.

Here’s a test of our iris model, whose residuals we visualized above:

ncvTest(m1)

Non-constant Variance Score Test 
Variance formula: ~ fitted.values 
Chisquare = 2.493218, Df = 1, p = 0.11434

For proof of method, see “References” section in documentation

Meanwhile, here’s a Breusch-Pagan test of the heteroskedastilistic data above. Notice the p-value:

ncvTest(lm(z~x, data = het))

Non-constant Variance Score Test 
Variance formula: ~ fitted.values 
Chisquare = 27.79159, Df = 1, p = 1.3511e-07

Model comparison

We can use an F-statistic to compare models when we add or omit variables. Section 9.2 of OpenIntro contains a great introduction to model selection. In it, they recommend two different model selection strategies:

1. Backwards elimination - where we generate a fully saturated model, then take one variable out at a time.

2. Forward selection - where we start with a single predictor variable, and add one new variable at a time.

With each step in either of these processes, we need some kind of test to help us evaluate if the removal/addition of a variable has improved the model.

In OpenIntro, they use R². But we can also use an F-test.

F-test

Use anova(aModel, anotherModel) to compute the F-statistic for the comparison of two models.

Further up on this page, we created a model that aimed to predict iris sepal length using measures of iris petal length.

Here’s that model’s summary:

summary(m1)

Call:
lm(formula = Sepal.Length ~ Petal.Length, data = iris)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.24675 -0.29657 -0.01515  0.27676  1.00269 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   4.30660    0.07839   54.94   <2e-16 ***
Petal.Length  0.40892    0.01889   21.65   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4071 on 148 degrees of freedom
Multiple R-squared:   0.76, Adjusted R-squared:  0.7583 
F-statistic: 468.6 on 1 and 148 DF,  p-value: < 2.2e-16

We may wonder if using a quadratic formula renders a better model:

m1_quadratic <- lm(Sepal.Length ~ Petal.Length + I(Petal.Length^2), data = iris)
summary(m1_quadratic)

Call:
lm(formula = Sepal.Length ~ Petal.Length + I(Petal.Length^2), 
    data = iris)

Residuals:
    Min      1Q  Median      3Q     Max 
-1.0684 -0.2348  0.0121  0.2049  0.9146 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)        5.05833    0.14036  36.038  < 2e-16 ***
Petal.Length      -0.16435    0.09427  -1.743   0.0834 .  
I(Petal.Length^2)  0.08146    0.01318   6.181 5.96e-09 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3639 on 147 degrees of freedom
Multiple R-squared:  0.8095,    Adjusted R-squared:  0.8069 
F-statistic: 312.3 on 2 and 147 DF,  p-value: < 2.2e-16

Compare the two outputs and notice that our Adjusted R-squared has increased. This is a good sign.

But an F-statistic quantifies the difference in model fit between two models:

anova(m1, m1_quadratic, test = "F")

Analysis of Variance Table

Model 1: Sepal.Length ~ Petal.Length
Model 2: Sepal.Length ~ Petal.Length + I(Petal.Length^2)
  Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
1    148 24.525                                  
2    147 19.466  1    5.0593 38.206 5.955e-09 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

If you want to know more about how this test is performed, this article by Danielle Navarro is a great place to look.

The main thing of importance when performing an F-test on two models is that the smaller of the two models (the “null” model) cannot contain variables that are not in the larger model (the “alternative” or “full” model).