DGHI/Biostat Lab: Lab 3 (705)

LAB MATERIALS

R Markdown file for Lab 3 Click link to download. Fill it in with your answers to the following lab tasks. When you’re ready to submit, name it as Lab3_FirstinitialYourlastname.Rmd, and submit it using the Sakai dropbox.
Excel document with Tables 1, 2, and 3
Lab_3_kenya.rds - data file available on Sakai

Lab 3 Goals

Assess the bivariate relationships between outcome and covariables and the statistical association between each of the two variables
Estimate the epidemiologic measures of association (risk difference, risk ratio and odds ratio) between risk factors and outcome

Lab 3 Grading scheme

Competency	Points
.Rmd file runs without error	10
Task 3 (Table 1)	5
Task 4 (Table 2)	10
Task 5 (Table 3)	20
Task 6 (stratified boxplots)	10 (5 each)
Task 7 (short answer)	5
Task 8 (short answer)	10
Task 9 (short answer)	5
Task 10 (short answer)	5
Task 11 (short answer)	20
Total	100

Task 1: Load libraries and dataset

For this assignment, we’ll need packages {tidyverse}, {skimr}, {epiR}, {tableone}, and {epiAssist}

For your data, you will use the dataset Lab_3_kenya.rds, located in the Sakai Resources folder for this course. This has all of the variables that we’ve created in labs 0, 1, and 2, and only contains those observations in our closed cohort (n = 16,828).

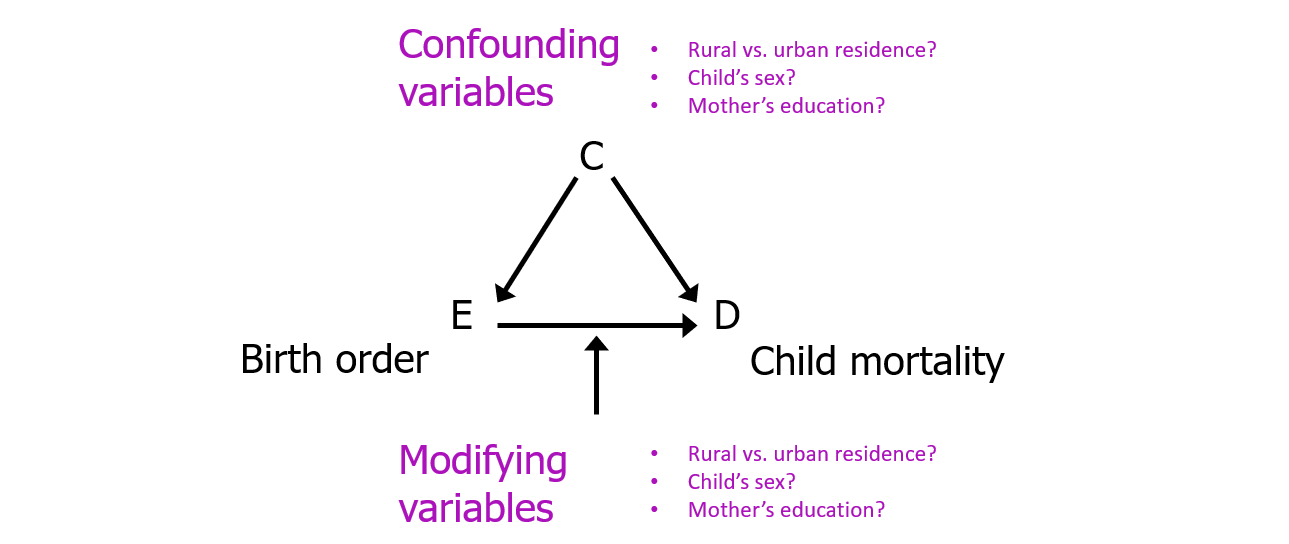
Task 2: BIG PICTURE

Just think on this for a moment. Internalize it. Come back to it:

For this and subsequent labs, we are considering

Child mortality within 5 years as our outcome (response) variable
Birth order >= 5 as the main risk factor variable and
Other variables as potential confounders or modifiers of the relationship between mortality and birth order.

Causal diagram of birth order (E: “exposure”) on childhood mortality (D: “disease”)

Task 3: Table 1

Tabular analysis of continuous variables by mortality status

INSTRUCTIONS: Fill in Table 1 with the descriptive statistics for maternal BMI (mbmi) and maternal age (mage), overall and by the two levels of child mortality within 5 years (death).

This table also requires you to use R to calculate statistical tests (T-test and Kruskal-Wallis) of the association between the outcome, death, and maternal BMI and age (i.e., comparing the distributions of maternal BMI and maternal age for the children who died versus those who were alive).

Round p-values to 3 decimal places.

Read on for advice on how to generate overall and stratified summary statistics, as well as instructions for how to perform the two statistical tests.

Overall summary statistics for each variable variable

The skim() function provided by {skimr} makes this task a simple one. However, unlike previous labs where we ran a summary on the entire dataset, in this task we want individual variables. To keep your output clean, we recommend you generate your summary statistics only for the variables of interest.

We can use a pipe with skimr() to call specific variables, like this:

data %>%
  skim(variable)

Stratified summary statistics

Since we’re already doing things in a pipe, we can use the filter function to retrieve summary statistics based on mortality status. To stratify by the variable death, we should add the group_by() function to our pipeline, specifying that we want to “group by death, then skim the variable mbmi”:

data %>%
  group_by(death) %>%
  skim(mbmi)

Note: Table 1 asks for counts of records with mbmi and mage data available vs. those missing, both overall and by the 2 levels of death (i.e. dead and alive). If you look closely, this means that we need counts of counts of kids with data available on mbmi and mage, overall, within levels of death, and those missing values. skim() does not give you raw counts of the variable death that account for those missing values.

Use table() or a pipe, group_by() and count() to get the counts of children in each group of death (i.e. by levels of death). Then use the column of your skim output, n_missing, to subtract missing values from groups

T-tests and Kruskal-Wallis tests

T-tests and one of their nonparametric cousins, Kruskal-Wallis, can be used to compare means between between groups (i.e. between sub-populations), with the null hypothesis (H₀) being that all means are equal.

There are a few simple functions from the {stats} package that we can use to manually run these tests. To implement, we use functions t.test() and kruskal.test(). Both take the same arguments:

A formula: depVar ~ indepVar
A data frame

In this case, we are interested in knowing whether or not the means for mbmi and mage differ by strata of child mortality status, death.

What this means is that when we’re building our formula, the “y”/dependent variable (the resulting means), should be on the left, while the “x”/independent variable (a categorical stratifying variable), should be on the right.

Formulas: In R, “formulas” follow different rules depending on the function. As a general rule, most take the form y ~ x. Go here to learn more.

Example of T-tests and Kruskal-Wallis

As an example, we might use the starwars dataset, available through the {dplyr} package (in the tidyverse), to inspect the body mass of different characters by gender. Let’s take a look at the raw data:

name	height	mass	hair_color	skin_color	eye_color	birth_year	sex	gender	homeworld	species
Luke Skywalker	172	77	blond	fair	blue	19.0	male	masculine	Tatooine	Human
C-3PO	167	75	NA	gold	yellow	112.0	none	masculine	Tatooine	Droid
R2-D2	96	32	NA	white, blue	red	33.0	none	masculine	Naboo	Droid
Darth Vader	202	136	none	white	yellow	41.9	male	masculine	Tatooine	Human
Leia Organa	150	49	brown	light	brown	19.0	female	feminine	Alderaan	Human
Owen Lars	178	120	brown, grey	light	blue	52.0	male	masculine	Tatooine	Human

Our formal question might look like this: “Does mean character height differ by a character’s gender?” (For the purposes of example, assume that the 83 characters are a sample from a large population of characters)

We can calculate summary statistics for sub-group frequency counts and means:

starwars %>%
  filter(!is.na(gender)) %>%
  group_by(gender) %>%
  summarize(n = n(), mean = mean(height, na.rm = TRUE))

gender	n	mean
feminine	17	164.6875
masculine	66	176.5161

We can also visualize the respective distributions of height by gender using density plots.

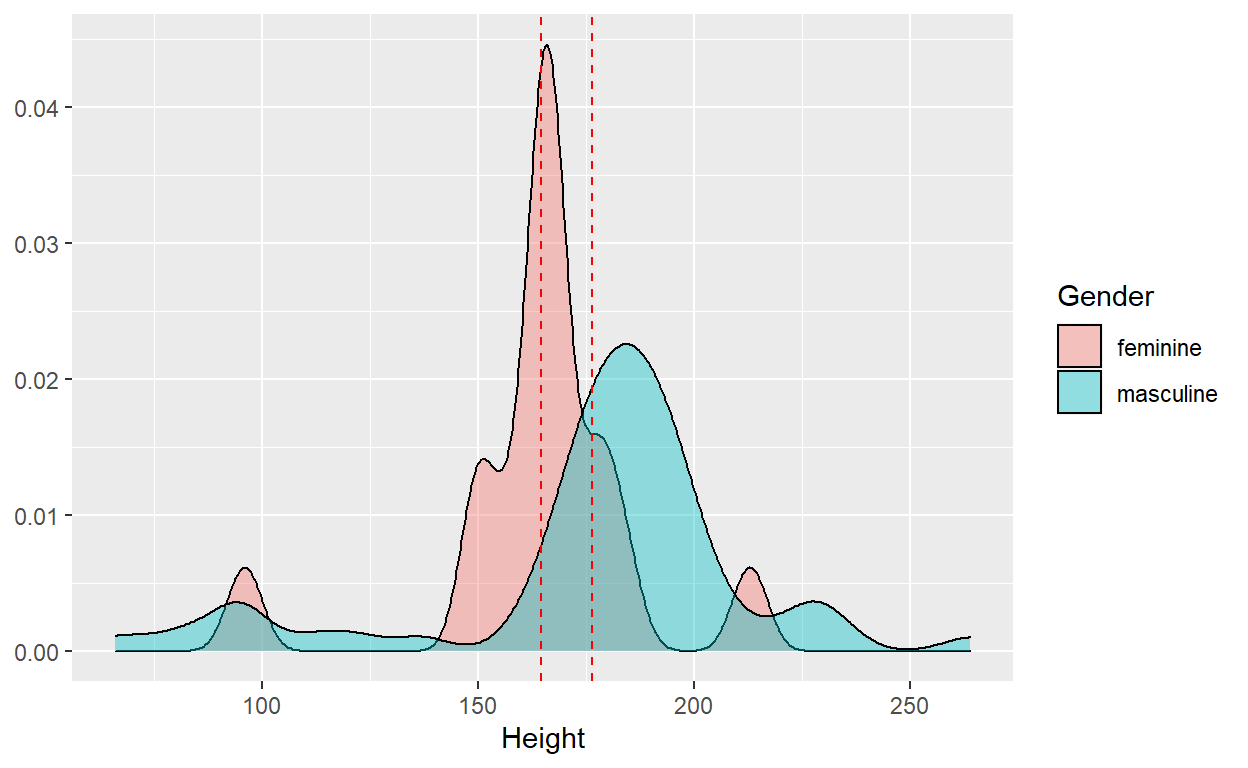
Our t-test would effectively tell us whether or not the observed difference in sample mean of height supports the conclusion that the population mean height is different between the two groups.

t.test(height ~ gender, data = starwars)

#>  Welch Two Sample t-test
#>
#> data:  height by gender
#> t = -1.5596, df = 37.315, p-value = 0.1273
#> alternative hypothesis: true difference in means between group feminine and group masculine 
#> is not equal to 0
#> 95 percent confidence interval:
#>  -27.191682   3.534423
#> sample estimates:
#>  mean in group feminine mean in group masculine 
#>                164.6875                176.5161

Function output is indicated by lines that start with #>

However, since the category for gender == 'feminine' only contains 17 observations, we might decide that a nonparametric test (one that doesn’t assume a normal distribution), might be more appropriate for the small sample size. In this case we can use the Kruskal-Wallis test:

kruskal.test(height ~ gender, data = starwars)

#> Kruskal-Wallis rank sum test
#> 
#> data:  height by gender
#> Kruskal-Wallis chi-squared = 8.6845, df = 1, p-value = 0.003209

Note that our decision tree for statistical tests of continuous outcome variables would get us to the Wilcoxon Rank Sum Test. In R, this is implemented the same as the Kruskal Wallis test, but uses the function wilcox.test(). We have used kruskal.test() because this is the test we will perform for Table 1.

Notice the difference in the conclusion you would draw from either test. For the t-test, we should conclude that we cannot reject the null hypothesis, whereas the nonparametric test tells us that there is a statistically significant difference in the mean height of the two groups.

Tabular analysis of categorical variables by `death`

INSTRUCTIONS: Table 2 contains three distinct columns for frequency counts and percentages.

The first, “All Children” requires the overall frequency counts and percentages by the categorical variables of interest. These are the same values that you generated for Table 1 in both labs 1 and 2.

The next two columns, “Dead” and “Alive”, require frequency counts and percentages of each of the variables of interest, stratified by mortality status at 5 years, death. Be sure to calculate percentages only for the non-missing values and round percentages to 1 decimal place.

This table also includes statistical measures (Chi-Sq and Fisher’s exact test) of the association between mortality status and the variables in the table.

Round p-values to 3 decimal places.

{tableone} package

We will complete this task by first using the package {tableone}, a powerful tool for tabular analysis, especially for stratified analyses like this one.

The function CreateTableOne() will create a {tableone} object that generates mean and standard deviation for continuous variables, and frequency counts and percentages for factor variables.

CreateTableOne() requires several arguments of central importance for it to run:

1.) vars = - a vector of variable names, written as strings
2.) strata = - a categorical variable for stratifying (if desired)
3.) data = - your data frame
4.) factorVars = - used to convert character variables to factors on the fly

factorVars: You shouldn’t need to use factorVars = for your kenya data, since we have already converted categorical variables to factors in the previous labs.

Create a vector of variables

For starters, we’ll need a vectorized list of our variables of interest, written as strings (in quotes).

As an example, we might use the derived variables in our kenya dataset for size and pnc. To make our code more readable, we will create a vector object that contains both variable names. To do this, we put both variable names in quotes, separating them by commas within a vector, c(). Then we need to assign the vector a name so that we can call it later. Here, we’ve named the vector variables.

variables <- c('size', 'pnc')

Construct {tableone} objects

First, we will construct two different {tableone} objects: a “simple” table with univariate frequency counts, and a “stratified” table, with bivariate counts.

After that, we’ll use print() to view the output generated by those two different objects.

Simple table

For a simple table of summary statistics, we only need to use arguments vars = and data =. It’s best practice to assign the {tableone} object to a name, so that we can use it in a print() function in a moment.

simple_tab <- CreateTableOne(vars = variables, 
                             data = kenya)

Stratified table

We may also want to stratify our results by a second variable, like bord5.

stratified_tab <- CreateTableOne(vars = variables, 
                                 data = kenya, 
                                 strata = 'bord5')

Print table

We can then use a print() function, with arguments specific to our {tableone} object, to view our simple and stratified tables.

With categorical variables, it’s typically best to use the argument showAllLevels = TRUE so that we see every category.

Setting showAllLevels to FALSE will leave out the reference level for each variable.

Print simple table

print(simple_tab, showAllLevels = TRUE)

#>              level                  Overall      
#>  n                                   16828        
#>  size (%)     Very large                26 ( 7.4) 
#>               Larger than average       76 (21.7) 
#>               Average                  158 (45.1) 
#>               Smaller than average      65 (18.6) 
#>               Very small                25 ( 7.1) 
#>  pnc (%)      No prenatal care          15 ( 9.1) 
#>               Received prenatal care   149 (90.9)

Print stratified table with chi-square test of independence

Whereas the simple table prints overall frequency counts and percentages, our stratified table will take the stratifying variable (in the case of this example, bord5), and perform a chi-square test of independence for that stratifying variable and each of the variables of interest e.g. of size and pnc:

print(stratified_tab, showAllLevels = TRUE)

#>              Stratified by bord5
#>               level                  1-4 in Birth Order 5+ in Birth Order  p     test
#>  n                                   13263              3565                         
#>  size (%)     Very large                23 ( 9.3)          3 ( 2.9)        0.157     
#>               Larger than average       51 (20.6)         25 (24.5)                  
#>               Average                  108 (43.5)         50 (49.0)                  
#>               Smaller than average      50 (20.2)         15 (14.7)                  
#>               Very small                16 ( 6.5)          9 ( 8.8)                  
#>  pnc (%)      No prenatal care           4 ( 3.7)         11 (20.0)        0.002     
#>               Received prenatal care   105 (96.3)         44 (80.0)

Note that each row of the stratified results sum to the same result as given by the column for “Overall” in our simple_tab.

As the default for categorical variables, the {tableone} print() function performs a chi-square test of independence between `bord5’ and each of the variables of interest.

There’s one glaring issue here, however: neither of our stratified variables meet the assumption of normality! Each contains at least one cross-tabulation with counts that are less than 5.

Fisher’s exact test of significance

When we look at our decision tree for hypothesis testing of categorical outcome variables, we might decide that we need to use a Fisher’s Exact test when our data doesn’t meet the assumption of all expected cell counts being at least 5 for a chi-square test of independence.

You can use the output from chisq.test() to find expected cell counts:

size_tab <- table(kenya$bord5, kenya$pnc)
X2 <- chisq.test(size_tab)
X2$expected

To do this in a {tableone} object, we just need to include exact = TRUE in our print() function to calculate a Fisher’s Exact test, the nonparametric equivalent of the chi-square test of independence.

print(stratified_tab, showAllLevels = TRUE, exact = TRUE)

#>               Stratified by bord5
#>               level                  1-4 in Birth Order 5+ in Birth Order p      test 
#>  n                                   13263              3565                          
#>  size (%)     Very large                23 ( 9.3)          3 ( 2.9)        0.141 exact
#>               Larger than average       51 (20.6)         25 (24.5)                   
#>               Average                  108 (43.5)         50 (49.0)                   
#>               Smaller than average      50 (20.2)         15 (14.7)                   
#>               Very small                16 ( 6.5)          9 ( 8.8)                   
#>  pnc (%)      No prenatal care           4 ( 3.7)         11 (20.0)        0.001 exact
#>               Received prenatal care   105 (96.3)         44 (80.0)

Although in this particular example we draw the same conclusions from the Fisher’s exact test as we do from the chi-square test of independence, this will not always be the case.

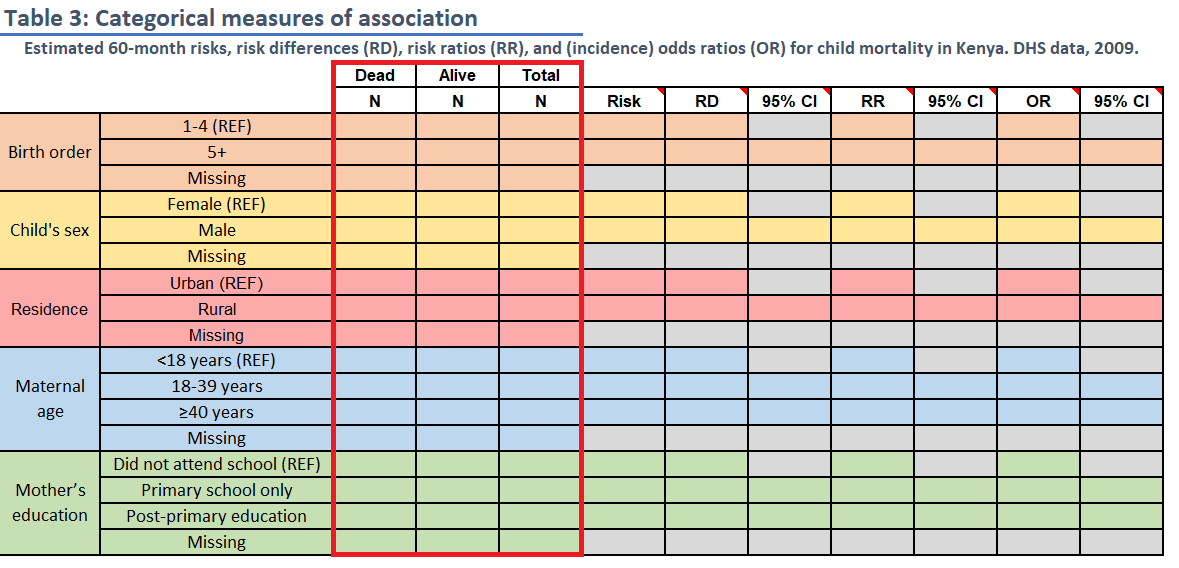
Task 5: Table 3

Risk Differences, Risk Ratios, and Odds Ratios

INSTRUCTIONS: Fill in Table 3 with frequency counts overall and by levels of child mortality within 5 years and with the stratum-specific risk of death (these are the same frequency count values, N, as in Table 2). Then use mAssoc() to compute the risk difference, risk ratio and the odds ratio of death comparing levels for each of the 5 variables to the reference level.

We use mAssoc() in the package {epiAssist} to generate these values. This function is a helper function for the original epi.2by2() function, which is available in the package {epiR}. epi.2by2() works the same as mAssoc(), except it only provides output for a single index/reference level pair. mAssoc() can do multiple index levels all at once.

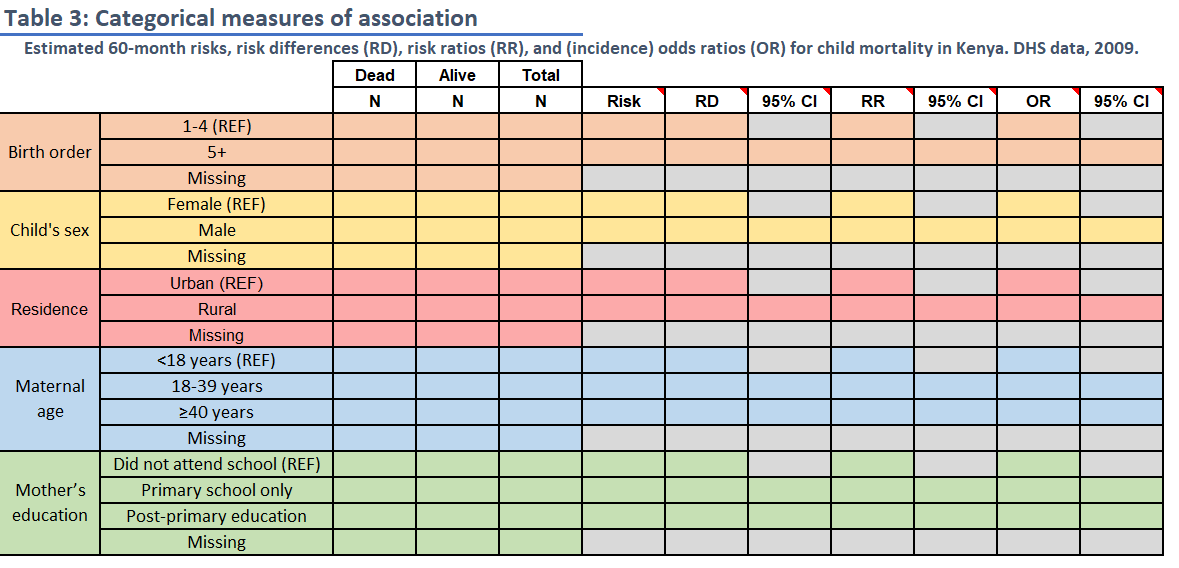
The reference level for each variable is noted in the spreadsheet (“REF”). For the two 3-level variables, calculate risk differences and ratios for each non-reference level relative to the reference level.

Round risks to 3 decimal places and ratios to 2 decimal places.

Take a deep breath.

Don’t let this table overwhelm you. We’re going to break it down step-by-step

Frequency counts

The frequency counts in this table align with those generated for Table 2. Feel free to use Excel equations to transfer data from sheet 2 to sheet 3.

Risk

The value for risk should be calculated as the risk of the outcome of interest (death == "Dead") according to each level of the exposure. Risk should be reported as a proportion, rounding to the third decimal.

Risk difference (RD), Risk Ratio (RR), and Odds Ratio (OR)

RD, RR, and OR are what are known as “measures of association” because they are used to compare outcomes between levels of a categorical variable. In epidemiology, we refer to the baseline level as the “reference level” and the comparator level as the “index level”.

In practical terms, for things like RRs and ORs, the index level goes in the numerator and the reference level goes in the denominator.

You can use your underlying knowledge of these measures of association to calculate our answers by hand and confirm the results that we’ll obtain using the functions that follow.

`mAssoc()` for Measures of Association

For this task, we will use mAssoc() to generate all three measures of association (RD, RR, and OR) in a singular output.

To use mAssoc(), we must take several steps to ensure that our data is in the proper shape for our measures to be calculated appropriately:

1.) Create a table object using table()
2.) Rearrange the table with flipTable() to put it in the appropriate alignment for use by mAssoc()
3.) Submit our rearranged table to mAssoc().

mAssoc()’s main input is a table object arranged in the following format:

#   -----------  ----------  ----------
#                Outcome +   Outcome -
#   -----------  ----------  ----------
#     Expose +   cell 1      cell 3          
#     Expose -   cell 2      cell 4
#   -----------  ----------  ----------

As a way of demonstrating, we will use the variable bord5, stratified by death to calculate our measures of association.

Step 1: Create a table object with `table()`

First, we need to generate a table object and assign it a name. Keep in mind that we want our exposure variable (in this case, bord5) along the left side of the table and our outcome variable (death) at the top of the table.

tab_bord5 <- table(kenya$bord5, kenya$death)
tab_bord5

#>                      Alive  Dead
#>  1-4 in Birth Order 11809  1454
#>  5+ in Birth Order   3002   563

Step 2: Rearrange table with `flipTable()`

Notice that mAssoc() takes a table object with the cross-tabulation of outcome of interest (Outcome +) and exposure of interest (Expose +) in the top-left cell:

Reminder that the function mAssoc() is a wrapper function for the epi.2by2() function from package {epiR}.

#   -----------  ----------  ----------
#                Outcome +   Outcome -
#   -----------  ----------  ----------
#     Expose +   cell 1      cell 3          
#     Expose -   cell 2      cell 4
#   -----------  ----------  ----------

If we refer to our tableof bord5 and death, we’ll notice that it currently displays the inverse of the arrangement required by mAssoc():

tab_bord5

#>                       Alive  Dead
#>  1-4 in Birth Order  11809   1454
#>  5+ in Birth Order    3002    563

That is, our tabulation of bord5 currently takes the following form, with “Outcome-” and “Expose-” in the top-left corner. We need “Outcome+” and “Expose+” in that corner:

#   -----------  ----------  ----------
#                Outcome -   Outcome +
#   -----------  ----------  ----------
#     Expose -   cell 1      cell 3          
#     Expose +   cell 2      cell 4
#   -----------  ----------  ----------

To fix this, we can use flipTable(), assigning it back to the same name for the table object:

tab_bord5 <- flipTable(tab_bord5)

tab_bord5

#>                      Dead  Alive
#>  5+ in Birth Order    563   3002
#>  1-4 in Birth Order  1454  11809

Generate measures of association with `mAssoc()`

To generate our measures of association and their accompanying confidence intervals, all we need to do is submit our rearranged table to mAssoc(), specifying that our data is cohort data with method = "cohort.count", and setting our confidence level to 0.95 with conf.level = .95:

mAssoc(tab_bord5, method = "cohort.count", conf.level = 0.95)

#> MEASURES OF ASSOCIATION FOR:  5+ in Birth Order (index) vs.  1-4 in Birth Order (referent)
#> Point estimates and 95% CIs:
#> -------------------------------------------------------------------
#> Inc risk ratio                                 1.44 (1.32, 1.58)
#> Odds ratio                                     1.52 (1.37, 1.69)
#> Attrib risk in the exposed *                   0.05 (0.04, 0.06)
#> Attrib fraction in the exposed (%)            30.58 (24.05, 36.56)
#> Attrib risk in the population *                0.01 (0.00, 0.02)
#> Attrib fraction in the population (%)          8.54 (6.20, 10.82)
#> -------------------------------------------------------------------
#> Uncorrected chi2 test that OR = 1: chi2(1) = 62.125 Pr>chi2 = <0.001
#> Fisher exact test that OR = 1: Pr>chi2 = <0.001
#>  Wald confidence limits
#>  CI: confidence interval
#>  * Outcomes per population unit

Reading `mAssoc()` output:

The output of interest from mAssoc() will be printed to the console. You can find it by clicking on the area with a red square around it in this screenshot:

If we set units = 100, our attributable risk in the exposed (risk difference) would be interpretable as a difference of x number of outcomes per 100 people in the index level when compared to the reference level. Since our population unit is set to 1, this number is simply interpreted as an individual’s risk difference of experiencing the outcome if they are in the index level of the exposure.

Here is a quick guide to the components of the output relevant to this activity:

Inc risk ratio: Our basic risk ratio
Odds ratio: Our basic odds ratio
Attrib risk in the exposed: The risk difference. mAssoc() takes another argument, units =, which by default is set to 1. This regulates our output for the measure of risk difference.

`mAssoc()` when exposure variable has 3+ levels

Now that you’ve seen the code for bord5 as an example, if you’re paying close attention, you may have started to wonder, “But what about variables like education, when there’s more than one index level?”

Good news: flipTable() and mAssoc() are designed to handle exposure variables with any number of levels. This means that the steps you take for bord5, male, and rural will also apply to magec and education; simple as that.

Running mAssoc() when your exposure variable has 2+ levels will render multiple outputs for each respective index variable. The person who wrote this function was even nice enough to label each of those levels and whether or not they are the index or the reference level.

Task 6: Side-by-side boxplots

INSTRUCTIONS: Generate boxplots of maternal BMI (mbmi) and maternal age (mage), stratified by levels of child mortality (death).

For this activity, we need boxplots that plot continuous variables based on child mortality. In ggplot2, we can stratify boxplots by using a second categorical variable when we specify our aesthetics (aes()). In other words, if you set mbmi to the y-axis, you can use a categorical variable, like death as the variable on the x-axis.

Additionally, don’t forget to label your axes, give the plot a title, and save it using ggsave()

Within your call to geom_boxplot(), you can also change the color with fill = "colorname". Find a list of color names here

Here’s an example of what we are looking for, using the starwars dataset. We’ve adjusted the dimensions a bit to accommodate one lone outlier. Care to guess who it is?

Task 7: Short answer

For Table 1, what is the null hypothesis being tested for each the two variables. Do the two statistical tests agree? Is there a statistically significant difference in the distributions of either BMI or age by child mortality? Are there substantively/clinically significant differences in these distributions? If statistical and substantive differences disagree, why might that be the case?

Task 8: Short answer

For Table 2, what is the null hypothesis being tested for the variables. Do the two statistical tests agree? Is there a statistically significant difference in any of these bivariate distributions? Are there substantively/clinically significant differences in these distributions?

Task 9: Short answer

Age has been evaluated both as a continuous and categorical variable. Do the tests of association for these 2 parameterizations of age agree? If not, why not?

Task 10: Short answer

For Table 3, which risk factor has the strongest association with mortality? Provide a rationale for this assessment. Which factors are protective and which are harmful?

Task 11: Short answer

Prepare a brief paragraph describing and interpreting risk, RD and RR estimates (from Table 3) for the 60 month risk of death in association with birth order and maternal age.

Begin the paragraph by reporting the overall risk or proportion of deaths in the study population. Don’t just repeat numbers that are already shown in the table; note the values of effect estimates you feel should be highlighted, but otherwise describe the results in words. Write this paragraph as if you were including it in the results section of a manuscript. (175 words maximum).